ne reprenant que les formules vues pour la première fois en e.c.e. Les démonstrations des résultats précédés d'une étoile (*) sont à connaître.
algèbre linéaire
formule du rang : pour f linéaire de E dans F : dim(ker(f)) + dim(im(f)) = dim(E)
formule du binôme : avec A et B matrices carrées qui commutent
:
techniques de base
suites numériques calculables
(un) SA de raison r 
"
n un+1
= un + r
(*) " n un = u0 + n.r
(un) SG de raison r "
n un+1 = r.un (*)
"
n un = u0.rn = u1.rn-1
(un) SAG un+1 = a.un + b : (*) un
- a = an.(u0 - a
) avec a tel que a
= a.a + b (a 
1)
(un) SLR2T un+2 = a.un+1
+ b.un :
l'équation caractéristique r2 = a.r +b a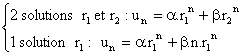 
sommations (x différent de 1)
(*) 
(*)
(*)
nombres 
: 
est
le nombre de parties à p éléments d'un ensemble à
n éléments
si 0 <
p < n ,
= 0 si p < 0 ou p > n
analyse
séries
· séries géométrique
et dérivées :
 |
 |
· série exponentielle :
· série de Riemann :
la série de terme général 
,
n Î N*, est convergente ssi a
> 1, divergente ssi a £
1
équivalents classiques
(*) ex - 1 ~0 x
(*) ln(1 + x) ~0 x
(*) ln(x) ~1 x - 1
voir aussi D.L.
intégrales
sommes de Riemann : avec f continue sur [a, b] :
formule de Taylor avec reste intégral pour f de classe Cn+1 sur I intervalle, a et t appartenant à` I :
développements limités (D.L) au voisinage de 0
(
)
par substitution
de -x à x
par intégration
du D.L. de 
par substitution
de -x à x
qui fournit
les D.L. de
probabilités
conditionnement P(A/B) = PB (A) = 
avec P(B) 
0
formule des probabilités composées : P(A
B)
= P(A).P(B/A)
(Ai) système complet d'événements
:"i, P(Ai) différent de 0
; " i différent de j, Ai
Aj
= 
; 
= 
formule des probabilités totales : avec (Ai) système complet d'événements
| X v.a. discrète
|
X v.a. de densité f
|
|
|
couple de v.a. discrètes
loi du couple : pij = P(X = xi et Y = yj)
pour tout xi Î X(W
) et tout yj Î Y(W
)
cov(X,Y) = E([X - E(X)][Y - E(Y)]) (def)
= E(XY) -E(X)E(Y) (thm)
V(X + Y) = V(X) + V(Y) + 2cov(X,Y) généralisation :
coefficient de corrélation linéaire : rX,Y
= 
lois discrètes usuelles
· X v.a certaine : X(W ) = {c}; P(X = c) = 1 E(X) = c V(X) = 0
· X suit la loi de Bernoulli B(1,
p) de paramètre p Î ]0, 1[ ssi
:
X(W ) ={0, 1}; P(X = 1) = 0 ; P(X = 0) =
1 - p.
E(X) = p V(X) = p(1 - p).
· X suit la loi binomiale B(n,
p) avec n Î N, p Î
]0, 1[ ssi :
X(W ) = [[0, n]] ; "
k Î [[0, n]], P(X = k) = 
X est le nombre de succès lors de n épreuves identiques
et indépendantes, la probabilité du succès à
chaque épreuve étant p.
(*) E(X) = np (*) V(X) =
np(1- p).
· X suit la loi hypergéométrique
H
(N, n, p) avec n, N ÎN*, p Î
]0, 1[ ssi :
X(W ) Ì
[[0, n]] ; " k Î
[[0, n]] , P(X = k) =
X est le nombre d'individus présentant le caractère étudié
dans un échantillon de n individus pris parmi N , le caractère
étudié ayant la fréquence p dans la population des
N individus.
(*) E(X) = np
· X suit la loi uniforme sur [[1,n]]
ssi X(W ) = [[1, n]] et "
k Î [[1, n]] P(X = k) = 1/n.
· X suit la loi de Poisson P(l
), avec l > 0, ssi :
(*) E(X) = l
(*) V(X) = l
· X suit la loi géométrique
G(p),
avec p Î ]0, 1[, ssi :
X est le temps d'attente du premier succès au cours d'épreuves
successives et indépendantes.
lois continues usuelles
· X suit la loi uniforme U([a,
b]) ssi X a pour densité f telle que :
X a pour fonction de répartition F telle que :
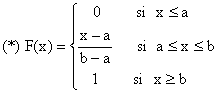
· X suit la loi exponentielle
E(a ), avec a
> 0, ssi X a pour densité f telle que :
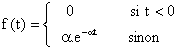
X a pour fonction de répartition F telle que :
· X suit la loi normale N(m,
s
), avec m ÎR,
s
> 0, ssi X* = 
suit la loi normale N(0, 1) de f.r :
.
E(X) = m V(X) = s2
Inégalité de Bienaymé-Tchébicheff
Pour X v.a d'espérance m et de variance s2
:
fonctions de deux variables
| f(x0, y0) extremum local de f | Þ p = q = 0 ( en (x0, y0) ) |
| p = q = 0, rt - s2 > 0, r > 0 | Þ f(x0, y0) minimum local |
| p = q = 0, rt - s2 > 0, r < 0 | Þ f(x0, y0) maximum local |
| p = q = 0, rt - s2 < 0 | Þ f(x0, y0) n'est pas un extremum local |
| p = q = 0, rt - s2 = 0 | : on ne peut rien dire |
