retour à l'accueil
retour à l'index cours
 

I. Généralités

Une suite (u_n)_nÎN est dite :
croissante ssi : " n Î N u_n+1 ³ u_n ;
décroissante ssi : " n Î N u_n+1 £ u_n ;
majorée par M  R ssi : " n ÎN u_n £ M ;
minorée par m  R ssi : " n ÎN u_n ³  m ;
convergente vers L ÎR ssi " e >0 $ N Î N n ³ N Þ ê u_n - L  ê< e .

Théorème 1. Une suite croissante et majorée est convergente.Une suite décroissante et minorée est convergente.

Deux suites (u_n)_nÎN et  (v_n)_nÎN sont dites adjacentes ssi une d’elles est croissante, l’autre décroissante, et

Théorème 2. Deux suites adjacentes sont convergentes et elles ont même limite.

^{Techniques et conseils}

Pour montrer que (u_n) est croissante, ou décroissante :
* utiliser la définition ;
* étudier le signe de u_n+1 – u_n : à utiliser si u_n se présente ‘comme une somme’ ;
* pour une suite à termes positifs : comparer u_n+1/u_n à 1 :   pour tout n, u_n+1/u_n ³ 1  (u_n) croissante.
A utiliser si u_n se présente ‘comme un produit’ ;
* pour une suite u_n+1 = f(u_n) : voir ci dessous.

Pour montrer que (u_n) est majorée, ou minorée :
* manipulation des inégalités.
* pour une suite u_n+1 = f(u_n) : voir ci dessous.

Théorème 3. (Algèbre des limites.) Soit (u_n) convergeant vers L , (v_n) convergeant vers L' , a ÎR. Alors :

(u_n + v_n) converge vers L + L' ; (a u_n) converge vers a L.

(u_n v_n) converge vers L L' ;

(u_n/v_n) converge vers L/L' si de plus L' est non nul...

Théorème 4.Soit (u_n) convergeant vers L et f continue en L . Alors ( f(u_n) ) converge vers f(L).

Théorème 5. (Passage à la limite dans les égalités, les inégalités.)

a) Soit u_n + v_n = a , lim_{n® +¥}(v_n) = 0. Alors lim_{n® +¥}(u_n) = a.
b) Soit u_n £ v_n , lim_{n® +¥}(u_n) = L, lim_{n® +¥}(v_n) = L '. Alors L £ L '.
c) Soit u_n £ v_n, lim_{n® +¥}(u_n) = +¥ . Alors lim_{n® +¥}(v_n) = +¥ .
d) Soit u_n £ v_n, lim_{n® +¥}(v_n) = -¥ . Alors lim_{n® +¥}(u_n) = ....
e) Soit u_n £ v_n£ w_n , lim_{n® +¥}(u_n) = lim_{n® +¥}(w_n) = L. Alors lim_{n® +¥}= L.
 
 

II. Suites u_n+1 = f(u_n)

DEUX (et pas plus !) théorèmes de cours :

Théorème 1 : Si (u_n) I intervalle et si f est CROISSANTE sur I, alors (u_n) est MONOTONE.

Théorème 2 : Si (u_n) converge vers L et si f est continue en L, alors la L vérifie nésessairement : L = f(L).

Démonstration théorème 1 :
Cas où u₀ £  u₁ : On démontre " n ÎN u_n  £ u_n+1 par récurrence :

u0 £ u1 et un £ un+1	f (un ) £ f(un+1) car f est croissante sur I
	un+1 £ un+2.

Cas où u₀ ³  u₁ : On démontre " n ÎN u_n   ³ u_n+1 par récurrence :

u0  ³ u1 et un ³ un+1	f (un ) ³ f(un+1) car f est croissante sur I
	un+1 ³ un+2.

Démonstration théorème 2 :
Supposons que (u_n) converge vers L : lim_{n® +¥}(u_n) = L . Alors lim_{n® +¥}f(u_n) = f(L) car f est continue en L. D'autre part lim_{n® +¥}(u_n+1) = L . En passant à la limite dans l'égalité u_n+1 = f(u_n), on obtient le résultat annoncé.
 

Techniques et conseils

* L'étude de l'équation f(x) = x, de l'inéquation f(x) £ x , souvent proposée par l'énoncé, est toujours capitale:
- L'équation f(x) = x fournit les points fixes de f, c'est à dire, si f est continue, les points vers lesquels la suite (u_n) peut éventuellement converger (théorème 2).
- L'inéquation f(x) £  x fournit la position de la courbe C_f par rapport à la première bissectrice (droite d'équation y = x).

* On montre (u_n)  I, (u_n) majorée, minorée, bornée, en général par récurrence, en utilisant les points fixes de f.

* Si (u_n)  I et f(x) ³  x pour tout x  I, alors (u_n) est croissante. C'est évident !

* A cause du théorème 2, le cas ou f est croissante est de loin le plus agréable. Dans le cas général, l'énoncé peut proposer d'utiliser la formule des accroissements finis (A.F). L'idée générale est la suivante :

Les hypothèses (que l'énoncé demande de vérifier dans les premières questions) :
(u_n) Ì I ; L Î I et f(L ) = L ; ½ f '½£  k < 1 sur I ;
impliquent successivement :
½ f(u_n) – f(L ) ½£ k.½ u_n - L½ (A.F) ;
½ u_n+1 -L½£ k.½ u_n -L½ ( car f(u_n) = u_n+1 et f(L ) = L ) ;
½ u_n - L½£  kⁿ .½ u_n - L½ (récurrence) ;
lim_{n® +¥}(u_n) = L (car 0 < k < 1, donc lim_{n® +¥}(kⁿ) =0).
De plus, u_n est une valeur approchée de L à moins de kⁿ près.
 

III. Séries

1°) Définitions. Soit (u_n)_nÎN une suite de nombres réels. La série de terme général u_n est la suite des sommes partielles (S_n)_nÎN , définie par :

On dit que la série de terme général u_n est convergente ssi la suite (S_n) est convergente, et la limite S de la suite (S_n) est alors appelée somme de la série. On note :

2°) Séries usuelles

· Série géométrique et séries géométriques dérivées
Théorème 1. a) La série de terme général xⁿ_, n ÎN¸ est convergente ssi ½ x½ < 1, de somme 1/(1 - x) :

b) La série de terme général nx^n-1_, n ÎN*¸ est convergente ssi ½ x½ < 1, de somme 1/(1 - x)² :

c) La série de terme général n(n-1)x^n-2_, n ³ 2 ¸ est convergente ssi ½ x½ < 1, de somme 2/(1 - x)³ :

d) Les séries de terme général nxⁿ_, n ÎN*, et n²xⁿ, n ÎN*, sont convergentes ssi ½ x½ < 1, et :

Dem. a) Pour n Î N* et x Î R, considérons S_n(x) = 1 + x + x² + ... + xⁿ. On a :

Si x ¹ 1, il vient :

(c'est l'identité géométrique), et si½ x½ < 1, comme lim_{n® +¥}(xⁿ⁺¹) = 0, on obtient :

ce qui prouve le résultat annoncé pour ½ x½ < 1. Pour ½ x½³ 1, le terme général xⁿ de la série ne tend pas vers 0, elle ne converge donc pas (voir plus loin, critères de convergence d'une série.)

b) Pour n Î N* et x ÎR, considérons T_n(x) = 1 + 2x + ... + nx^n-1. On a :

On a 1 + x + ... + x^n-1 = S_n-1(x), donc si ½ x½ < 1, lim_n®¥(1 + ... + x^n-1) = 1/(1-x) d'après le a). D'autre part, si ½ x½ < 1, lim_n®¥(nx^n-1) = 0. On obtient donc en passant à la limite n®¥: lim_n®¥( (1 - x)T_n(x) ) = 1/(1-x), puis le résultat annoncé pour ½ x½ < 1. Pour ½ x½³ 1, le terme général nx^n-1 de la série ne tend pas vers 0, donc...

c) même principe que pour a) et b), on pose :

mais l'explicitation de (1-x)U_n(x) devient (?) obscure. Il est nécessaire de raisonner sur les S , et effectuer un changement d'indice de sommation :

On effectue le changement d'indice i = k-1 dans la première somme, et i = k dans la deuxième ! Il vient

Le terme en i = 1 figure dans la première somme, mais pas dans la deuxième, le terme en i = n figure dans la deuxième, mais pas dans la première. Les autres termes se factorisent deux par deux, et on obtient :


Pour ½ x½ < 1, T_n-1(x) tend vers 1/(1-x)² et n(n - 1)x^n-2 tend vers 0, et la conclusion en résulte dans ce cas là.
Pour ½ x½³ 1, ...
d) Soit x tel que ½ x½ < 1. La série de terme général n x^n-1, nÎ N*, converge vers 1/(1-x)²_, donc la série de terme général n xⁿ = x n x^n-1, n ÎN*, converge vers x /(1-x)². D'autre part, pour tout k ÎN*, on a :
k² x^k = k (k-1) x^k + k x^k = k (k-1) x^k-2 x² + k x^k-1 x ; donc :

Supposons maintenant ½ x½ < 1. D'après c), U_n(x) tend vers 2/(1-x)³ , et d'après b), T_n(x) tend vers 1/(1-x)², quand n tend vers +¥ . La série de terme général k² x^k, k Î N*, est donc convergente, et

Pour ½ x½³ 1...

Techniques et conseils

* Les deux formules :


sont à savoir par coeur, ainsi que leurs démonstrations. La première formule, l'identité géométrique, peut être considérée comme un cas particulier de la formule qui donne la somme de termes consécutifs d'une suite géométrique : pour (u_n) SG de raison r ¹ 1 (et avec p > q) :

(u_q : premier terme de la somme ; p - q + 1 : nombre de termes dans la somme). Entraînez vous à utiliser cette formule pour calculer les sommes suivantes :

Rep :


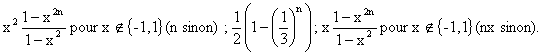
* A partir de :

on retrouve facilement :

puis :

en dérivant formellement par rapport à x les deux membres de la première égalité, puis en recommençant. Formellement, car il n'est pas du tout évident, et pas toujours vrai, que la dérivée d'une somme infinie soit la somme infinie des dérivées. Toujours est-il que :
la dérivée de x^k est kx^k-1 pour k ¹ 0, 0 pour k = 0 ;
la dérivée de 1/(1-x) = (1-x)^-1 est (-1) (-1) (1-x)^-2 = 1/(1-x)² ;
la dérivée de kx^k-1 est k(k-1)x^k-2 pour k ³ 2, 0 pour k = 1 ;
la dérivée de 1/(1-x)² = (1-x)^-2 est (-1)(-2)(1-x)^-3 = 2/(1-x)³...
and so on, ce qui fait apparaître des factorielles et des combinaisons...

· Séries de Riemann

La série de terme général 1/n^a , n ³ 1, est convergente ssi a > 1.
En particulier la série de terme général 1/n est divergente, et sa limite est +¥ (série harmonique).
La démonstration se fait par comparaison avec une intégrale généralisée, voir chapitre VI.

· Série exponentielle
Théorème Pour tout x dans R, la série de terme général xⁿ/n! est convergente, de somme e^x :

Dem a) Montrons d'abord que la série de terme général xⁿ/n! est convergente, et pour cela, utilisons les critères de convergence pour les séries, voir plus loin. Il suffit de montrer que la série est absolument convergente. Soit donc x ³ 0 fixé.Considérons n₀ dans N tel que x/n₀ soit plus petit que 1/2. On a alors, pour tout n ³ n₀ :

Chacun des facteurs x/(n₀+1), ... , x/n est inférieur à 1/2, et il y a n- n₀ tels facteurs, donc :

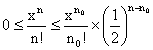
La série géométrique de terme général (1/2)ⁿ est convergente, il en résulte (voir plus loin, critères de convergence pour les séries à termes positifs) que la série de terme général xⁿ/n! est convergente.
b) Le programme demande d'admettre que la série en question a pour somme e^x, c'est pourtant tout-à-fait à notre portée, grâce à la formule de Taylor avec reste intégral, voir chapitre VI ! Faisons cette démonstration, à titre d'exercice. Comme la fonction exponentielle est de classe C^¥ , la FTRI s'applique pour tout n dans N, et comme exp⁽ⁿ⁾(x) = exp(x), il vient :

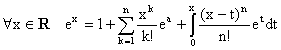
Si x ³ 0, on a :

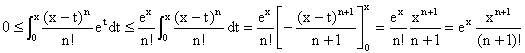
La série de terme général xⁿ/n! est convergente, nous venons de le voir, son terme général tend donc vers 0, voir plus loin ! Il en résulte que le reste intégral de la FTRI ci-dessus tend vers 0, et par passage à la limite dans la FTRI, on obtient le résultat. Si x £ 0, on a :

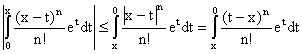
et la suite est analogue (faites la !)
 

3°) Critères de convergence pour les séries

· Opérations sur les séries convergentes : Si les séries de termes général u_n et v_n sont convergentes, de sommes respectives S et S', et si a ÎR, alors les séries de terme général u_n + v_n et a u_n sont convergentes, de sommes respectives S + S' et aS.

· Un critère négatif : Si la série S u_n converge, alors lim_n®¥(u_n) = 0.
Dem : Avec S_n = , on a u_n = S_n - S_n-1.
Il s'agit d'un critère négatif, dans la mesure on l'utilise pour montrer qu'une série n'est pas convergente. Par exemple la série de terme général 1, ou n, ... n'est pas convergente. Attention, si u_n tend vers 0, on ne peut rien dire : S 1/n diverge, S 1/n² converge. On peut aussi utiliser cette propriété pour montrer que u_n tend vers 0 : il suffit que la série S u_n soit convergente, voir une telle utilisation plus haut !...

· Séries à termes positifs, critères de comparaison

Théorème 1
0 £ u_n £ v_n ; S v_n converge Þ S u_n converge
0 £ u_n £ v_n ; S u_n diverge Þ S v_n diverge
Dem : Démontrons le premier point. Soit S_n = u₀ +u₁.+ ... + u_n. La suite (S_n) est croissante car
S_n+1 -S_n = u_n+1 ³ 0, et elle est majorée, car

La conclusion en résulte. Démonstration analogue pour le deuxième point.

Théorème 2
Soit u_n ³ 0, v_n³ 0, u_n ~_¥ v_n. Alors S u_n et S v_n sont de même nature,
c'est-à dire simultanément convergentes ou divergentes.

· Séries à termes quelconques

Définition La série S u_n est dite absolument convergente ssi la série S½ u_n½est convergente.

Théorème 3 (admis)Une série absolument convergente est convergente.

Techniques et conseils

· Bien retenir le principe de la démonstration du théorème 1, qui est souvent demandée dans un cas particulier. On a encore le résultat si on a u_n £ v_n seulement à partir d'un certain rang. Ce théorème peut être utilisé sous la forme suivante :
Théorème 4 Si u_n ³ 0, v_n³ 0, u_n = o(v_n) en +¥ et S v_n convergente, alors S u_n est convergente.
Exemple :
e^-n = o(1/n²), e^-n  ³ 0, 1/n² ³ 0 et S 1/n² convergente, donc S e^-n convergente. (Ce qui peut aussi se montrer en remarquant que e^-n est le terme général d'une série géométrique...)

· Ces quatre théorèmes tombent en défaut pour des suites qui ne sont pas à termes positifs : donc, les appliquer uniquement à des séries à termes positifs, et bien signaler que les séries sont effectivement à termes positifs.

· Bien répondre à la question posée : s'il sagit de calculer la somme d'une série, les critères de convergence ne suffisent pas, on revient alors à la définition et on utilise les techniques de base (dominos...), ou on fait apparaître la série étudiée comme combinaison linéaire de séries usuelles...

· Bien veiller à distinguer la série de terme général u_n, et la suite de terme général u_n. Par exemple :
La suite de terme général 1/n, n ÎN* est décroissante et converge vers 0.
La série de terme général 1/n, n ÎN* est croissante et tend vers +¥ .
 

IV. Autres types de suites

·Suites définies par une intégrale, comparaison d'une série et d'une intégrale : voir chapitre VI, calcul intégral

· Suites définies implicitement : Il s'agit d'étudier des suites définies par une condition du type f_n(u_n) = 0. Les outils principaux sont :
* Le théorème des valeurs intermédiaires pour l'existence (et l'unicité..) de u_n, n fixé. Voir chapitre I.
* Si f est croissante sur I intervalle et si f(a) <  f(b), avec a, b  I, alors a £ b. On utilise cette propriété (évidente…) pour étudier la variation de la suite (u_n) ou pour majorer, minorer la suite (u_n). Par exemple, avec f_n décroissante pour tout n, u_n vérifiant f_n(u_n) = 0, si f_n+1(u_n) < 0, alors la suite (u_n) est décroissante… Un petit tableau de variation rend la chose claire :

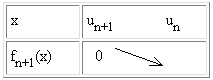
* La définition même de u_n , car c'est le seul renseignement qu'on ait : u_n est défini de façon implicite, et on n'aura pas d'expression explicite de u_n.

· Autres suites :
* On peut rencontrer des suites "atypiques", du genre u_n+1 = f(n, u_n). Lire attentivement l'énoncé, et répondre aux questions posées…
* Devant une expression du type u_n = , penser aux sommes de Riemann, voir chapitre VI.

D'une manière générale, le calcul intégral fournit une aide précieuse et essentielle à l'étude des suites et des séries. L'exemple le plus frappant de cette relation est la formule de Taylor avec reste intégral. Voir chapitre VI (cours) et chapitre I (exercices).

retour début