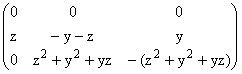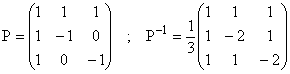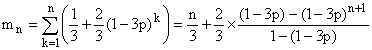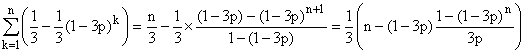exercice 1

1°) a) Le plus simple est de remarquer que la fonction sin est concave sur [0, p /2] (sa dérivée seconde, - sin, est négative sur I = [0,p /2]), sa représentation graphique est donc au dessus de ses cordes ; or la corde définie par les points (0, 0), et (p /2, 1) a pour équation y = (2/p) t. Donc sin(t) ³ (2/p )t, t £ (p /2) sin(t) pour t Î I. Sinon on étudie j (t) = (p /2)sin(t) - t sur I ( attention il est nécessaire de passer par j '').
b) du a) il résulte, pour tout t Î I : 0 £ t² cos^2kt £ (p /2)² sin²t cos^2kt = (p²/4) (1 - cos²t) cos^2kt. D'où le résultat en intégrant sur I et en utilisant la linéarité de l'intégrale.
c) Puisqu'on nous le dit ... Bien entendu, u(t) = sin t, v'(t) = (2k+1) (- sin t) cos^2kt. Ne pas omettre de dire que u et v sont de classe C¹. La partie toute intégrée est nulle, on utilise cos²t + sin²t = 1 puis la linéarité de l'intégrale, pour trouver I_k+1 = (2k+1)(I_k - I_k+1), et finalement :

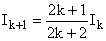
d) Il en résulte :

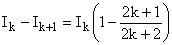
Donc d'après b) :

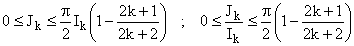
(On peut diviser par I_k qui est > 0 : I_k = j (p /2) - j (0) avec j '(t) = cos^2k+1t > 0 sur [0, p /2[.) Par encadrement, on obtient alors le résultat.

2°) a) Avec u = cos^2kt, v' = 1, u' = 2k (- sin t) cos^{2k- 1}t, v = t (u,v de classe C¹ sur I) :

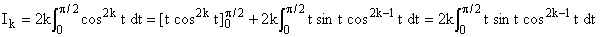
Avec u = sin t cos^{2k- 1}, v' = t, v = t²/2,
u' = cos^2kt - sin²t (2k- 1) cos^{2k- 2}t = cos^2kt + (cos²t - 1) (2k- 1) cos^{2k- 2}t = 2k cos^2kt - (2k-1) cos^{2k- 2}t :

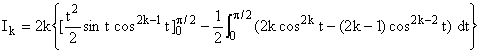
I_k = k( (2k- 1)J_{k- 1} - 2kJ_k )
b) On divise la relation précédente par I_k :

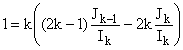
D'après 1°)c) :

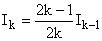
Par conséquent :

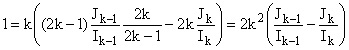
D'où le résultat.
c) I₀ = p /2 ; J₀ = p³/24... Soit u_k =J_k/I_k.

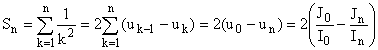
J_n/I_n tend vers 0 d'après 1°), et donc S_n tend vers 2 J₀/I₀ = 2 ´p³/24 ´ 2/p = p²/6 quand n tend vers +¥ . Nous pouvons donc écrire :

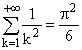
d) Après ce beau résultat, nous retombons dans les trivialités (utiles) ! : k(k+1) ³ k² ³ k(k- 1) > 0, donc...Mais

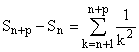
et l'encadrement précédent fournit :

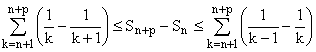
En étant attentif à ces nouveaux dominos :

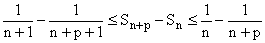
Avec p ® +¥ , par encadrement on obtient : 1/(n+1) £ S - S_n £ 1/n, puis : - 1/n £ S_n - S £- 1/(n+1), puis :

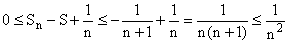
e) Il suffit de prendre n tel que 1/n² £ 10-⁶, soit n ³ 1000.
program essec;
var s : real ; k : integer ;
BEGIN
s := 0 ;
for k := 1 to 1000 do s := s + 1/sqr(k) ;
s := s +0.001 ;
writeln(s) ;
END.
et toc !

Un bien bel exercice strictement dans les limites du programme et qui établit de façon élémentaire un résultat non trivial. Ce résultat est établi classiquement en utilisant les séries de Fourier. Une autre démonstration utilise des techniques assez lourdes de trigonométrie. Celle-ci paraît originale...
Le deuxième exercice est moins folichon...

Exercice 2
Partie I
1°) a)
.
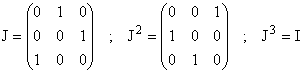b) c) Pour tout M(x,y,z) de E, M(x,y,z) = xI + yJ + zJ², donc E est un sev de M₃(R), de famille génératrice (I, J, J²).
xI + yJ + zJ² = 0 Þ M(x,y,z) = 0 Þ x = y = z = 0, cette famille est donc libre et est donc une base de E.

2°) a) M(x,y,z) ´ M(x',y',z') = (xI + yJ + zJ²) ´ (x'I + y'J + z'J²).
En développant et en utilisant J³ =I, J⁴ = J, on obient
M(x,y,z) ´ M(x',y',z') = (xx'+yz'+zy')I + (xy'+yx'+zz')J + (xz'+yy'+zx')J² appartient à E. OUI, les matrices M(x,y,z), M(x',y',z') commutent...
b) Yaka remplacer dans l'égalité ci dessus x' par x² - yz, etc, on trouve :
M(x,y,z) ´ M(x^2-yz, z^2-xy, y^2-zx) = (x³ + y³ + z³ - 3xyz)I
Le développement (plus ou moins) patient de (x+y+z)[(x- y)² + (y- z)² + (z- x)²] conduit à 2x³ + 2y³ + 2z³- 6xyz, d'où la conclusion :
M(x,y,z) ´ M(x^2-yz, z^2-xy, y^2-zx) = (1/2) (x+y+z)[(x- y)² + (y- z)² + (z- x)²] I (1)
c) Si x+y+z ¹ 0 et x, y, z "pas tous égaux", alors a = (1/2) (x+y+z)[(x- y)² + (y- z)² + (z- x)²] ¹ 0, donc d'après (1) M(x,y,z) est inversible, d'inverse (1/a) M(x²-yz, z²-xy, y²-zx).
d) Réciproquement, si M(x,y,z) est inversible d'inverse M^-1, on obtient en multipliant (1) par M^-1 :
M(x²-yz, z²-xy, y²-zx) = a M^-1.
Supposons a = 0. On a alors M(x²-yz, z²-xy, y²-zx) = 0, donc x²-yz = z²-xy = y²-zx = 0 d'après 1°). 0n en déduit x² = yz, z² = xy, y² = zx, puis x³ = y³ = z³ , puis x = y = z (car la fonction qui à x associe x³ est une bijection de R sur R) , puis M(x,y,z) = x M(1,1,1) qui n'est pas inversible (deux colonnes égales).
Par conséquent a ¹ 0, et M est inversible ssi a ¹ 0.

3°) a) l valeur propre de M(x,y,z) Û$ X ¹ 0, [M(x,y,z) -l I]X =0 Û$ X ¹ 0, M(x-l ,y,z)X = 0 Û M -l I non inversible.
b) M(x - (x+y+z), y, z) = M(- y- z, y, z) n'est pas inversible d'après 2°) c), donc x+y+z valeur propre de M(x,y,z) d'après 3°) a).
Pour le sous espace-propre associé, on effectue L₃¬ L₁ + L₂ + L₃ sur la matrice M(-y-z, y, z), puis :
* si z ¹ 0, L₃ ¬ zL₃ - yL₂. On aboutit à la matrice

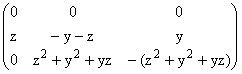
y² + z² + zy n'est jamais nul : considéré comme un polynôme du 2nd degré en y, son discriminant - 3z² est négatif,car z ¹ 0. En notant a, b, c les coordonnées des vecteurs propres, on a donc le système :

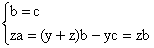
Donc a = b = c car z ¹ 0.
* si z = 0, on a le système :

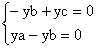
Si y ¹ 0, on retrouve a = b = c ; si y = 0, tout (a,b,c) de R² est solution.
En résumé, le sous-espace propre associé à la valeur propre x+y+z est Vect(1,1,1) si y, z "pas tous nuls", R³ sinon.
c) l valeur propre de M(x,y,z) Û M(x-l ,y,z) non inversible Û x - l + y +z = 0 OU x - l = y = z Û
l = x + y + z car y ¹ z. Avec une seule valeur propre, M(x,y,z) n'est pas diagonalisable, sinon il existerait P inversible telle que M(x,y,z) = P l I P-¹ = l I, donc x = l et y = z = 0 ; or y ¹ z...
d) Avec y = z, M(x,y,z) est symétrique donc diagonalisable. Les valeurs propres sont x + 2y et l tel que x - l = y, l = x - y.

4°) a) b) c) Après ces calculs quelque peu pénibles, le rythme s'accélère...On trouve

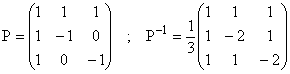
De M(x,y,z) = P D P^-1 on déduit comme d'habitude [M(x,y,z)]ⁿ = P Dⁿ P^-1 et des calculs sans surprise conduisent au résultat annoncé (les M(1,1,1) et M(2,- 1,- 1) ne sont là que pour faire joli ( et continuer l'exercice !), la "table de multiplication " des M(x,y,z) n'étant pas très appétissante...).

Partie II
1°) a) b) c) Zut alors, on ne nous laisse même pas le plaisir de citer cette fameuse formule ! Bref :
M = M(1- 2p, p, p)
En notant P_n la matrice colonne a_n b_n c_n :
P_n+1 = M P_n ; P_n = Mⁿ P₀
puis :
P_n = [(1/3) M(1,1,1) + (1/3) (1 - 3p)ⁿ M(2,- 1,- 1)]P₀
P₀ est la matrice colonne 1 0 0, P_n est donc la première colonne de la matrice Mⁿ.
Avec 0 < p < 1/2, il se trouve que - 1 < 1 - 3p < 1, donc a_n, b_n, c_n tendent, à la surprise générale, vers 1/3...

2°) a) X₁ + X₂ + ... + X_n est le nombre de passage en A entre les instants 0 et n, m_n le nombre moyen de passages entre les instants 0 et n...
On a m_n = E(X₁ + X₂ + ... + X_n) = m₁ + m₂ + ... + m_n (linéarité de l'espérance). Comme X_k suit une loi de bernoulli de paramètre m_k = P(X_k = 1) = P(A_k), on obtient :

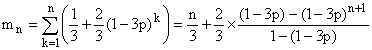
d'où le résultat annoncé. m_n est équivalent à n/3 (l'autre terme tend vers une valeur finie).
b) Mutatis mutandis, les nombre moyens de passage en B et en C entre les instants 0 et n sont :

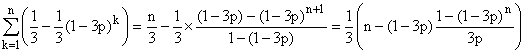
3°) a) Une jolie question. On va utiliser la formule des probabilités totales, mais avec quelque soin car la probabilité de base est une probabilité conditionnelle :

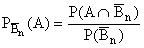
L'événement B_n+1 est la réunion disjointe des événements (A_n Ç B_n+1) , (B_n Ç B_n+1) , (C_n Ç B_n+1). Le deuxième est de probabilité (conditionnelle) nulle, et on a pour le premier :

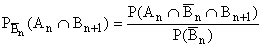
Donc :

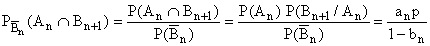
De même :

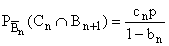
Finalement :

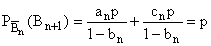
Pas si évident que ça...
b) T_B (W ) = N* ,et pour tout k Î N* :

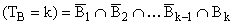
D'après la formule des probabilités composées généralisée :

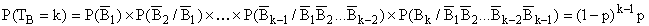
Donc T_B suit la loi géométrique de paramètre p, et E(T_B) = 1/p.
c) Idem pour T_C, car B et C jouent le même rôle par rapport à A.
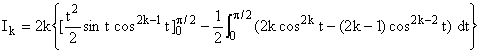
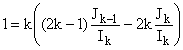
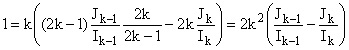
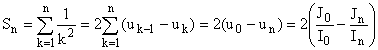
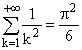
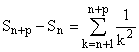
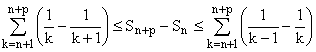
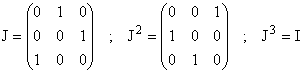