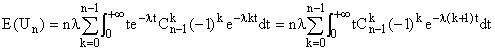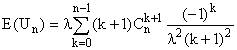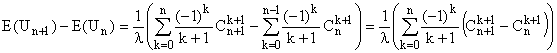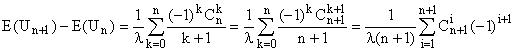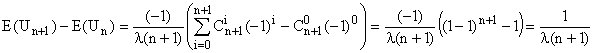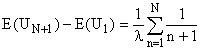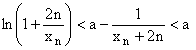Exercice 1.

1. 1.

1. Effectivement...
2. M(a)M(b) = I Û a + b - 3ab = 0 Û b(1 - 3a) = - a. Si a ¹ 1/3, M(a) est inversible, son inverse est a/(3a - 1). M(1/3) est la matrice dont tous les éléments sont égaux à 1/3, elle n'est donc pas inversible (deux colonnes proportionnelles).
3. M(a) est symétrique...
4. M(a₀)² = M(a₀) Û M(2a₀ - 3a₀²) = M(a₀) Û 2a₀ - 3a₀² = a₀ Û a₀ - 3a₀² = a₀(1 - 3a₀) = 0
Û a₀ = 1/3 car a₀ non nul.
5. (a) P est la matrice dont tous les éléments sont égaux à 1/3. Q est la matrice dont les éléments de la diagonale sont égaux à 2/3, les autres à - 1/3. L'équation proposée est équivalente à un système de deux équations, fort heureusement proportionnelles : 1 / 3 + 2 a / 3 = 1 - 2a ; 1 / 3 - a / 3 = a.
Solution : a = 1 - 3a.
(b) P² = P, Q² = Q, PQ = QP = 0.
(c) Avec la formule du binôme (P et a Q commutent) :
M(a)ⁿ = [P + a Q]ⁿ = S_k=0,nC_n^k P^k(a Q)^{n- k} = P + aⁿQ
(les autres termes sont égaux à 0, à cause de PQ = QP = 0). Finalement, M(a)ⁿ = P + (1 - 3a)ⁿQ.

1.2.

1. (a) En notant X_n la matrice colonne dont les éléments sont, de haut en bas, p_n, q_n, r_n , on a : X_n+1 = M(a) X_n, d'où, par récurrence : X_n = M(a)^{n- 1} X₁ (attention, on part de 1 !). Il s'agit finalement d'expliciter [P + (1 - 3a)^{n- 1}Q]X₁. Les termes sur la diagonale sont égaux à (1/3) (1 + 2(1 - 3a)^n-1), les autres à (1/3) (1 - (1 - 3a)^n-1).
(b) Avec a Î ]0, 2/3[, 1 - 3a a le bon goût d'être dans l'intervalle ]- 1, 1 [ :
0 < a < 2/3 Þ 0 < 3a < 2 Þ 0 > - 3a > - 2 Þ 1 > 1 - 3a > - 1 (il y a équivalence.)
(1 - 3a)^{n- 1} converge donc vers 0, et p_n, q_n r_n convergent tous joyeusement vers (p₁+q₁+r₁)/3...
2. (a) La formule des probabilités totales appliquée trois fois (aux événements M_n+1, S_n+1, B_n+1), avec le système complet d'événements (M_n, S_n, B_n) conduit à : X_n+1 = M(1/6) X_n , en désignant par X_n la matrice colonne m_n, s_n, b_n.
(b) On a donc, par récurrence : X_n = M(1/6)^{n- 1}X₁
(c) (m₁+s₁+b₁)/3 = (0+1+0)/3 = 1/3, et 1/6 Î ]0, 2/3[ : d'après tout ce qui précède, on conclut que les probabilités de hausse, de stabilité, de baisse le jour n tendent toutes vers 1/3 (et en fait ceci est indépendant de l'état initial.)

Un exercice qui ressemble fort à l'essec math 3 95.

Exercice 2

2.1.

1. P(T_i < t) = P(T_i £ t) = 1 - e^-lt.
2. N_t est le nombre de composants défaillants entre les instants 0 et t, les composants sont défaillants de façon indépendante (car les variables T_i sont indépendantes), avec la probabilité :
P(T_i < t) = 1 - e^-lt. Par conséquent, N_t suit la loi binomiale de paramètres n et 1 - e^-lt , d'espérance E(N_t) = n(1 - e^-lt).
3. E(N_t) est supérieur à n/2 ssi :
1 - e^-lt > 1/2 Û e-l^t < 1/2 Û -l t < ln(1/2) Û t > ln(2) / l .

2.2.

1. (S_n > t) = (T₁ > t) Ç (T₂ > t) Ç ... Ç (T_n > t)
2. Il en résulte : P(S_n > t) = (e^-lt)ⁿ = e ^-lnt, car les T_i sont indépendantes et de même loi exponentielle de paramètre l .
F_n(t) = P(S_n £ t) = 1 - P(S_n > t), donc F_n(t) = 1 - e^{-l nt} si t ³ 0, 0 sinon.
3. S_n suit la loi exponentielle de paramètre l n, d'espérance 1/(nl ), de variance 1/(nl )².

2.3.

1. (U_n < t) = (T₁ < t) Ç (T₂ < t) Ç .... Ç (T_n < t). Si, si !!
2. G_n(t) = (1 - e^-lt)ⁿ pour t ³ 0, 0 sinon. G'_n(t) =l e^-lt n (1 - e^-lt)^{n- 1} si t < 0, G'_n(t) = 0 si t < 0. La fonction g_n proposée convient..
3. Existence de E(U_n) : la fonction n l t e^-lt(1 - e^-lt)^{n- 1} est continue, ³ 0 sur [0, +¥ [, négligeable devant 1/t² en +¥ . L'intégrale de 1/t² sur [1, +¥ [ est convergente (Riemann), il en résulte que E(S_n) existe.
Calcul : on se précipite sur la formule du binôme pour développer (1 - e^-lt)^{n- 1}, puis on utilise la linéarité de l'intégrale, pour écrire :

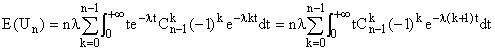
Pour k fixé, l'intégrale généralisée est convergente car absolument convergente, et on calcule sa valeur en effectuant une intégration par parties sur [0, x] avec u = t, v' = e-l^(k+1)t, puis on fait tendre x vers +¥ , et on trouve :

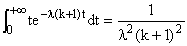
On se souvient alors de quelque chose dans le genre

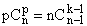
Ici :

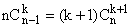
Il vient :

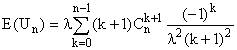
d'où le résultat annoncé. Ensuite :

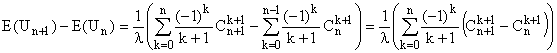
(On a C_nⁿ⁺¹ = 0)

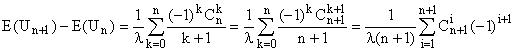
(Formule de Pascal - celle qui permet de construire le tableau de Pascal ; puis le 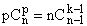 sous une autre forme - le recours aux factorielles est toujours possible ; puis changement d'indice i = k+1.)

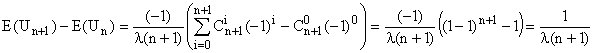
(On met - 1 en facteur, et formule du binôme. Etonnant, non ?)
4. On somme de n = 1 à n = N, pour obtenir

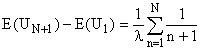
Et E(U_n) est équivalent à ln(n)/l lorsque n tend vers +¥ .

Exercice 3

3.1.

1. Evidemment, sans calculatrice, il s'agit uniquement de donner l'allure de la représentation graphique de f_1. Une étude minimale s'impose (est-elle demandée ?), en commençant par expliciter (sans se tromper !) f₁(x) :

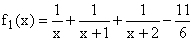
f₁ est strictement décroissante sur chacun des intervalles qui composent son "ensemble de définition" (notion un peu oubliée aujourd'hui...). L'important est de ne pas oublier de tracer les quatre asymptotes à la courbe, d'équations x = - 2, x = - 1, x = 0, y = - 11/6. On remarque qu'il y a trois solutions à l'équation f₁(x) = 0, donc à l'équation (E₁).
2. f₁(1) = 0, et alors ? ... Il faut y passer (ou alors passer à la question suivante...), ce sont bien les solutions exactes qui sont demandées, il faut résoudre l'équation f₁(x) = 0... Après réduction au même dénominateur, on développe, réduit et ordonne le numérateur. Ces passionnants calculs aboutissent à :
- 11x³ - 15x² + 14x + 12 = 0, équation du troisième degré dont une racine est 1 (ben oui, car f₁(1) = 0 ! ;-)... On peut donc factoriser par x - 1, et toute méthode acceptable (schéma de Horner ou factorisation à la main) aboutit à :
(x - 1)(11x² + 26x + 12) = 0
Le discriminant réduit permet de gagner "un peu" de temps (mais cette technique ne figure au programme d'aucune classe fréquentée par nos élèves...) et on aboutit aux trois solutions :

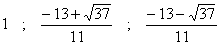
Les calculatrices sont interdites aux épreuves d'admission aux grandes écoles de commerce, ce n'est pas une raison de faire comme si elles n'existaient pas et n'avaient jamais existé...

3.2.

1. f_n est strictement décroissante sur chacun des 2n+2 intervalles qui composent son ensemble de définition.(Remarque : on lit dans le programme de e.c.e.1 : "Pour les résultats du cours, on se limite aux fonctions définies sur un intervalle de R. Les candidats doivent savoir étudier les situations qui s'y ramènent simplement.".) f_n décroît une fois de - 11/6 à -¥ , puis 2n fois de +¥ à -¥ , puis une fois de +¥ à - 11/6.
2. f_n est négative sur ]-¥ , - 2n[, et le théorème de la bijection appliqué à chacun des 2n+1 intervalles ]- 2n, - 2n+1[, ... , ]- 1, 0[, ]0, +¥ [ (2n+1 intervalles, c'est à dire autant qu'il y a de nombres entiers relatif de - 2n à 0) montre que l'équation (E_n) admet exactement 2n+1 solutions.

3.2.

1. x_n Î ]0, +¥ [.
2. Formule des accroissements finis pour la fonction qui à t associe  ln(t) sur l'intervalle [x - 1, x], puis on somme les inégalités obtenues en remplaçant x successivement par x+1, x+2, ... , x+2n. On fait ensuite x = x_n pour obtenir la dernière inégalité demandée.
3. L'inégalité demandée est équivalente à :
.
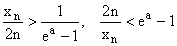Mais :

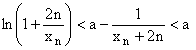
(car x_n est positif...), d'où le résultat en prenant l'exponentielle des deux membres.
4. lim_{n® +¥}(x_n) = +¥ ; lim_{n® +¥}ln(1 + 2n/x_n) = a par encadrement dans la dernière inégalité du 3.
5. 1 + 2n/x_n tend vers e^a, 2n/x_n tend vers e^a - 1, n/x_n tend vers (e^a - 1)/2, x_n est équivalent à :

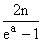
lorsque n tend vers +¥ .