exercice 1
1.1. 1°) 0 = M(0, 0) appartient à E et, pour tous a, b, a', b', a dans R :
M(a, b) + M(a', b') = M(a + a', b + b') , et a M(a, b) = M(a a, a b) appartiennent à E.
Donc E est un sous-espace vectoriel de M₃(R).
2°) Pour tout a, b Î R :

M(1, 0) et M(0, 1) constituent donc une famille génératrice de E, et cette famille est libre :
a ´ M(1, 0) + b ´ M(0, 1) = 0 Þ M(a, b) = 0 Þ a = b = 0.
C'est donc une base de E, qui est donc de dimension 2.
1.2. 1°) A² = I, donc A est inversible, et A-¹ = A.
2°) (A - l I)X = 0 conduit au système linéaire :

sur lequel on effectue les opérations L₂ « L₁, puis L₂ ¬ L₂ + l L₁, ce qui permet de se ramener au système triangulaire :

Les valeurs propres de A sont donc - 1 et 1.
3°) Le sous-espace propre associé à l = 1 est .

Le sous-espace propre associé à l = - 1 est .
La somme des dimensions des sous-espaces propres de A est 3, A est donc diagonalisable, et les trois vecteurs ci-dessus constituent une base de R³ dans laquelle la matrice de f_1,0 est de la forme voulue.
1.3. 1°) Les matrices de E sont symétriques réelles, donc diagonalisables.
2°) x u + y v + z w = 0 Þ

Donc C est une base de R³, car R³ est de dimension 3.
3°).

4°) La méthode du pivot aboutit à : 

5°) .
De même, M(a, b) ´ v = (b - a) ´ v, M(a, b) ´ w = (a - b) ´ w. Et donc
f_a,b(u) = (2b + a)u f_a,b(v) = (b - a)v f_a,b(w) = (a - b)u
6°) Le calcul précédent montre que u, v, w sont des vecteurs propres de f_a,b. Comme (u, v, w) est une base de de R³, f_a,b est donc diagonalisable, et D_a,b = diag( 2b + a, b - a, a - b ).
7°) La théorie de changement de base donne le résultat.
8°) D_a,b est diagonale, elle est donc inversible ssi les éléments de sa diagonale sont non nuls, ssi :
a - b ¹ 0 et a + 2b ¹ 0...
9°) ... et on a alors .

10°) M_a,b est inversible ssi 0 n'est pas valeur de M_a,b ssi a - b ¹ 0 et 2b + a ¹ 0.

exercice 2

2.1. 1°)pour tout x > - 1,

 donc h_n est strictement croissante.
2°) h_n(0) = 0 et h_n strictement croissante sur ]- 1, +¥ [, donc h_n < 0 sur ]- 1, 0[, h_n > 0 sur ]0, +¥ [.
3°) n = 1. a) f₁ est dérivable sur ]- 1, +¥ [ car c'est la somme de deux fonctions dérivables sur ]- 1, +¥ [.
Pour tout x Î ]- 1, +¥ [, f₁'(x) = h₁(x), donc f₁ est strictement décroissante sur ]- 1, 0], strictement croissante sur [0, +¥ [. Les limites ne posent pas de problème : en - 1, la limite de f₁ est +¥ , (" - 1´-¥ "), en +¥ aussi ( "+¥´ +¥ " ).
4°) n ³ 2. a) f_n est dérivable sur ]- 1, +¥ [ car c'est la somme de deux fonctions dérivables sur ]- 1, +¥ [.
f_n(x) = xⁿ ln(1 + x), donc 
b)

Les limites sont sans problèmes.

2.2.1 1°) Pour tout x Î [0, 1] :


Donc pour tout x Î [0, 1] : .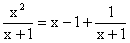
2°) .
3°) 
On a effectué une intégration par parties avec u = ln(1 + x), v' = x, u' = 1/(1 + x), v = x²/2. u et v sont de classe C¹ sur [0, 1] . (Attention à ne pas oublier ce point de rédaction.)

2.2.2. 1°) 
car sur [0, 1], xⁿ (x - 1) ln(1 +x) £ 0. La suite (U_n) est donc décroissante.
2°) " x Î [0, 1], xⁿ ln(1 + x) ³ 0, donc U_n ³ 0. La suite (U_n) est décroissante et minorée par 0, elle est donc convergente.
3°) Pour tout x Î [0, 1], 0 £ ln(1 + x) £ ln 2, donc 0 £ xⁿ ln(1 + x) £ xⁿ ln 2, donc

4°) D'après 3°), la suite (U_n) est encadrée pa r deux suites de limite nulle, elle converge donc vers 0.
2.2.3. 1°) On utilise l'identité géométrique, valable car - x ¹ 1 :

(En effet, - (- 1)ⁿ⁺¹ = (- 1)ⁿ⁺² = (- 1)ⁿ.)
2°) D'après la linéarité de l'intégrale :





3°) (*)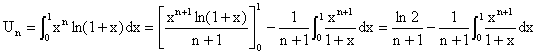
On a effectué une intégration par parties avec :

u et v de classe C¹ sur [0, 1].
Du 2°) on déduit :

En multipliant par (- 1)ⁿ, on obtient :

puis le résultat annoncé en remplaçant dans l'expression (*).

exercice 3
3.1. 1°) Les tirages ont lieu avec remise, X est donc le nombre de succès (obtenir une boule blanche) au cours de n épreuves identiques et indépendantes. A chaque épreuve, la probabilité du succès est 1/2, X suit donc la loi binomiale de paramètres n et 1/2, E(X) = n/2, V(X) = n/4.
2°) Pour 1 £ k £ n, (Y = k) est l'intersection des événements N₁, N₂, ... , N_{k- 1}, B_k, donc, par indépendance des lancers :
.
De même (Y = 0) est l'intersection des événements N₁, N₂, ... , N_n , donc
.
3°) Avec l'identité géométrique ( 1/2 ¹ 1) :

4°) soit

(x est différent de 1). S est dérivable en x (somme de fonctions dérivables), et

On remarque que la somme démarre valablement à k = 1, et on regroupe astucieusement les termes du numérateur (un terme en xⁿ⁺¹, un terme en xⁿ, un terme constant égal à 1) :
,
et on multiplie par x pour obtenir le résultat annoncé.
5°)

3.2. 1°) Z_p est le nombre de boules blanches obtenues au cours des p premiers tirages.
2°) X₁(W ) = {0, 1}, P(X₁ = 0) = P(X₁ = 1) = 1/2, E(X₁) = 1/2. (X₁ suit la loi de Bernoulli de paramètre 1/2.)
3°) Loi du couple (X₁, X₂) : X₁ et X₂ prennent leurs valeurs dans {0, 1}, et :
P(X₁ = 0 Ç X₂ = 0) = P(X₁ = 0) P(X₂ = 0 / X₁ = 0) = .

P(X₁ = 0 Ç X₂ = 1) = P(X₁ = 0) P(X₂ = 1 / X₁ = 0) = .

P(X₁ = 1 Ç X₂ = 0) = P(X₁ = 1) P(X₂ = 0 / X₁ = 1) = .

P(X₁ = 1 Ç X₂ = 1) = P(X₁ = 1) P(X₂ = 1 / X₁ = 1) = .

On en déduit la loi de X₂ en allant chercher dans la marge (en appliquant la formule des probabilités totales) :

P(X₂ = 0) = P(X₁ = 0 Ç X₂ = 0) + P(X₁ = 1 Ç X₂ = 0) = +=

P(X₂ = 1) = P(X₁ = 0 Ç X₂ = 1) + P(X₁ = 1 Ç X₂ = 1) =+ =

(Ou P(X₂ = 1) = 1 - P(X₂ = 0)...) X₂ suit aussi la loi de Bernoulli de paramètre 1/2.

4°) Z₂(W ) = {0, 1, 2}.
(Z₂ = 0) = (X₁ = 0 Ç X₂ = 0), donc P(Z₂ = 0) = .
(Z₂ = 2) = (X₁ =1 Ç X₂ = 1), donc P(Z₂ = 2) = .
(Z₂ = 1) = (X₁ = 0 Ç X₂ = 1) È (X₁ = 1 Ç X₂ = 0), ou P(Z₂ = 1) = 1 - [P(Z₂ = 0) + P(Z₂ = 2)] donne
P(Z₂ = 1) = 
5°) En p tirages, on peut obtenir 0, 1, ..., p boules blanches, donc Z_p(W ) = {0, ...., p}.

6°) a) Sachant Z_p = k :
* AVANT le tirage n°2, il y a 2 + c boules, avant le n°3, il y en a 2 + 2c, ... , avant le n° p+1, il y en a 2 + pc.
Parmi celles-ci, il y en 1 + kc qui sont blanches, car on a obtenu k fois une boule blanche.
Par conséquent, P(X_p+1 = 1 / Z_p = k) = 
b) La formule des probabilités totales avec le système complet d'événements (Z_p = k)_{0 £ k £ p} fournit alors :

c) La propriété à établir est vraie pour p = 1 d'après 3.2.2°), et pour p = 2 d'après 3.2.3°). Supposons que X₁, X₂, ..., X_p suivent la loi de Bernoulli de paramètre 1/2. Alors E(X_i ) = 1/2 pour 1 £ i £ p, donc
.
Le résultat du b) fournit alors :

Comme X_p+1(W ) = {0, 1} on en déduit que X_p+1 suit la loi de Bernoulli de paramètre 1/2.
La conclusion en résulte, d'après le principe de récurrence.
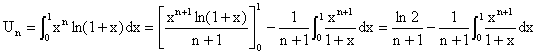