ecricome 2004 option économique : corrigé rapide

1. exercice

1.1.

1. Pour tout x Î R :

Donc f est paire.

2. Pour tout x, f(x) = (1 + x²)^–1/2, donc

Donc f est strictement décroissante sur [0, +¥[.

3.

4. D’après les résultats obtenus, on obtient le tableau de variations :

x	–¥ 0 +¥
f ‘(x)	+ 0 –
f(x)	0 ↗ 1 ↘ 0

Donc "x Î R, 0 £ f(x) £ 1.

Donc f est bornée sur R.

5. Une allure de cloche…

6. Sur [0, +¥[, f est continue strictement décroissante ; f(0) = 1 et lim_+¥ f = 0 ; donc f réalise une bijection de [0, +¥[ sur ]0, 1].

7. Pour tout y Î ]0, 1] :

8. Il semble bien que la bijection réciproque f^–1 soit la fonction de ]0, 1] dans [0, +¥[ définie par :

1.2.

1. Pour tout x Î R :

car si x ³ 0 alors x + |x| = x + x = 2x ³ 0, et si x £ 0, alors x + |x| = x + ( –x) = 0.

Donc

Et l’ensemble de définition de F est R.

2. F est dérivable sur R (car x ® x + Ö(x² + 1) est dérivable et positive sur R, et ln est dérivable sur ]0, +¥[ ), et, pour tout x Î R :

Donc F est une primitive de f sur R.

3. Pour tout x Î R,

Cette dernière égalité est vraie, donc F est impaire. On pouvait aussi utiliser la technique de la « quantité conjuguée » :

4. La limite de x + Ö(x² + 1) quand x tend vers +¥ est +¥, et la limite de ln(y) quand y tend vers +¥ est +¥, donc la limite de F en +¥ est +¥.

F est impaire et lim_+¥ F = +¥, donc lim_–¥ F = –¥.

5. Avec l > 0 :

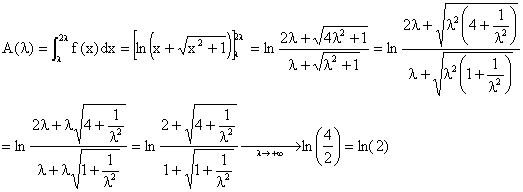
1.3.

1.

2. Le bon choix est u = x², u’ = 2x, v’ =x/Ö(1+x²), v =Ö(1 + x²) ; u et v sont de classe C¹ sur [0, 1] :

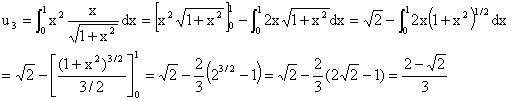
3. Pour tout x Î [0, 1], tout n Î N, 0 £ xⁿ⁺¹ £ xⁿ, donc

0 £ f(x) xⁿ⁺¹ £ f(x) xⁿ (car f ³ 0 sur [0, 1]), donc

0 £ I_n+1 £ I_n.

Ce qui prouve que la suite (I_n) est décroissante.

4. On a aussi démontré au 3°) que la suite (I_n) était minorée par 0, on en conclut que la suite (I_n) est convergente, sa limite ℓ étant ³ 0.

5. Pour tout x Î [0, 1], pour tout nÎ N, 0 £ xⁿ et Ö(1 +x²) ³ 1, donc

On utilise alors la positivité et la croissance de l’intégrale :

6. Par encadrement : lim_n®+¥ u_n = 0.

2. exercice

2.1

1. On utilise la méthode du pivot pour prouver que P est inversible et trouver :

2. a. Donner un résultat intermédiaire (soit PA, à multiplier à droite par P^–1, soit AP^–1, à multiplier à gauche par P) :

b.

3. De T = PAP^–1 on tire, avec n ³ 3 :

A = P^–1T P, Aⁿ = (P^–1T P) … (P^–1T P) (n facteurs), Aⁿ = P^–1TⁿP = 0.

4. a. On ne garde dans le développement que les termes de degré £ 2 :

b. On déduit du a : E(t) E(–t) = E(t – t) = E(0) = I. Donc E(t) est inversible et

E(t)^–1 = E(–t) = I – tA + (t²/2)A²

c. On montre : "n Î N, [E(t)]ⁿ = E(nt) par récurrence : la propriété est vraie pour n = 0, n = 1, et si on la suppose vraie pour n fixé dans N, alors

[E(t)]ⁿ⁺¹ = [E(t)]ⁿ E(t) = E(nt) E(t) = E(nt + t) = E( (n + 1)t ).

la propriété est vraie pour n + 1. La conclusion en résulte, et on a donc

[E(t)]ⁿ = E(nt) = I + nt A + (nt)²/2 A².

2.2.

1. Commençons par déterminer les valeurs propres de B, c'est-à-dire les valeurs de l telles que la matrice B – lI ne soit pas inversible. En effectuant les opérations élémentaires

L₁ « L₂ ; L₂ ¬ lL₁ + 2L₂

on obtient la réduite de Gauss :

Les valeurs propres de B sont donc 1, 2 (ce dont on pouvait se douter, vu la matrice D…).

B possède 2 valeurs propres distinctes, donc B est diagonalisable.

2. Déterminons un vecteur propre associé à chacune des valeurs propres :

Pour la valeur propre 1, le système est :

2x + 2y = 0 ; 0 = 0

Donc (1, –1) vecteur propre pour la valeur propre 1.

Pour la valeur propre 2 :

2x + y = 0 ; 0 = 0

Donc (1, –2) vecteur propre pour la valeur propre 2.

D’après la théorie du changement de base, la matrice

est inversible et telle que Q^–1BQ = D.

3. Dans le droit fil des questions, on peut bien sûr écrire :

B = QDQ^–1

Bⁿ = (QDQ^–1) … (QDQ^–1) (n facteurs)

Bⁿ = QDⁿQ^–1,

se livrer au calcul de Q^–1 par la méthode du pivot, puis terminer les calculs, avec Dⁿ = diag(1, 2ⁿ).

On peut se dire aussi qu’un brave petit RPR fera aussi bien l’affaire… Effectivement, l’affaire est rondement menée… Faites le, c’est très instructif !

4. 5. Les règles du calcul matriciel nous permettent d’écrire :

6. a. Le point important est de savoir que, pour tout x Î R,

et on peut alors écrire, par exemple :

Idem pour les autres coefficients, ce qui donne le résultat.

b. E(t) = e^t E₁ + e^2t E₂ avec

c. E₁² = E₁ ; E₂² = E₂ ; E₁ E₂ = 0 ; E₂ E₁ = 0.

d. E(t) E(t’) = (e^t E₁ + e^2t E₂) (e^t’ E₁ + e^2t’ E₂)

= e^t+t’E₁² +e^t+2t’E₁E₂ + e^2t+t’E₂E₁ + e^2(t+t’)E₂²

= e^t+t’ E₁ + e^2(t+t’) E₂ = E(t + t’)

e. Idem que 2.1.4.b !

3. exercice

1.a. On utilise la formule des probabilités totales avec le système complet d’événements (A, B) :

P(E) = P(E/A)P(A) + P(E/B)P(B) = 0,1 ´ 0,7 + 0,05 ´ 0,3 = 0,085.

b. Il s’agit de calculer P(A/E) :

2. a. Pour tout k ³ 1, (L₁ = k) = A₁A₂ … A_k–1B_k È B₁B₂ … B_k–1B_k. Ces deux événements sont incompatibles, donc

P(L₁ = k) = P(A₁A₂ … A_kB_k+1) + P(B₁B₂ … B_kB_k+1)

Les choix des serveurs sont supposés indépendants les uns des autres, donc

P(L₁ = k) = (0,3)^k(0,7) + (0,7)^k(0,3).

b.

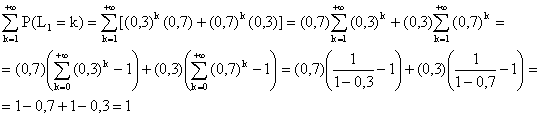
c. sous réserve de convergence (absolue) :

On a affaire à une combinaison linéaire de séries convergente (séries géométriques dérivées, de raison appartenant à ]–1, 1[), donc L₁ admet une espérance, et

d. Pour tous les couples (i, j) de N*² :

(L₁ = i Ç L₂ = j) = A₁ …. A_i B_i+1 …. B_i+j A_i+j+1 È B₁ …. B_i A_i+1 …. A_i+j B_i+j+1 .

Par incompatibilité, puis indépendance, on en déduit :

P(L₁ = i Ç L₂ = j) = (0,7)ⁱ (0, 3)^j (0,7) + (0,3)ⁱ (0,7)^j (0,3) = (0,7)ⁱ⁺¹ (0, 3)^j + (0,3)ⁱ⁺¹ (0,7)^j

e. En utilisant la formule des probabilités totales, avec les système complet d’événements (L₁ = i)_iÎN*, on obtient, pour tout j ³ 1 :

3. a. N_n est le nombre de succès (appeler le serveur A) au cours de n épreuves identiques et indépendantes, la probabilité du succès à chaque épreuve étant 0,7. Donc N_n suit la loi binomiale de paramètres n et 0,7.

On a E(N_n) = 0,7 n ; V(N_n) = 0,3 ´ 0,7 ´ n = 0,21 n.

b. T₁ est le temps d’attente du premier succès l’ors d’épreuves identiques et indépendantes, donc T₁ suit la loi géométrique de paramètre 0,7.

E(T₁) = 1/0,7 = 10/7 ; V(T₁) = (1 – 0,7)/(0,7)² = 30/49.

c. (T₂ = k) est l’intersection des deux événements (N_k–1 = 1) (le serveur A est appelé exactement 1 fois au cours des k – 1 premiers jours), et A_k (le serveur A est appelé le c^ène jour). Ces deux événements sont indépendants, donc

P(T₂ = k) = C_k-1¹ (0,7)¹ (0,3)^k-2 ´ 0,7 = (k – 1)(0,7)² (0,3)^k–2.

4.a. f_Z(t) = 0 si t £ 0 ; f_Z(t) = e^–t si t > 0.

F_Z(t) = 0 si t £ 0 ; F_Z(t) = 1 – e^–t si t ³ 0.

b. E(Z) = 1/1 = 1 seconde.

c. W = 1 + 0,1 Z.

d. Déterminons la fonction de répartition F_W de W. Pour tout x de R :

F_W(x) = P(W £ x) = P(1 + 0,1 Z £ x) = P(Z £ 10(x – 1) ).

Si x – 1 £ 0, c’est à dire si x £ 1, alors F_W(x) = 0.

Si x ³ 1, alors F_W(x) = 1 – e^{–10(x – 1)}.

F_W est continue, donc W est une variable aléatoire à densité.

si x < 1, F_W’(x) = 0 ; si x > 1, F_W’(x) = 10e^{–10(x – 1)}. Donc W admet pour densité f_W telle que

Si x £ 1, f_W(x) = 0 ; si x > 1, f_W(x) = 10e^{–10(x – 1)}.

e. W = 1 + 0,1 Z et l’espérance est linéaire, donc E(W) = 1 + 0,1 E(Z) = 1,1 (en euros ; c’est cher.)

5. a. f est positive ou nulle, continue sur R, et

Donc f est une densité de probabilité.

b. C’est déjà pratiquement fait : si x £ 0, F_X(x) = 0 ; si x ³ 0, F_X(x) = 1 – exp(–x²/2).

c. Sous réserve de convergence,

Soit x > 0 ; On effectue une intégration par parties avec :

u = t, v’= t exp(–t²/2), u’ = 1, v = –exp(–t²/2) ;

u et v sont de classe C¹ sur [0, x] : 

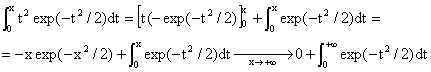
Donc, d’après le rappel fait :