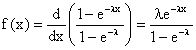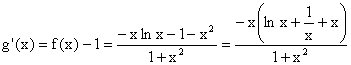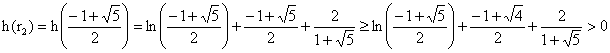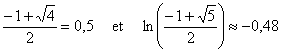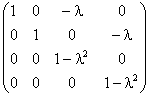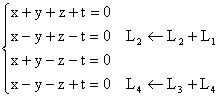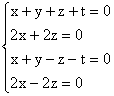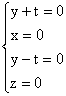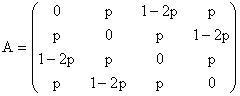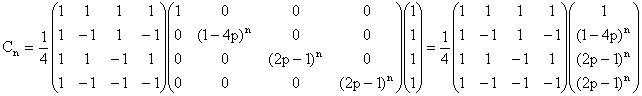exercice 1
1°) a) X qui suit une loi exponentielle prend ses valeurs dans R⁺, donc Y, partie entière de X, prend ses valeurs dans N.
b)

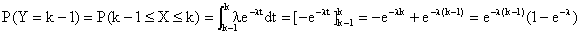
c) Y prend ses valeurs dans N, donc Y + 1 prend ses valeurs dans N*, et pour tout k appartenant à N* :
P(Y + 1 = k) = P(Y = k - 1) = (e-l )^{k- 1} (1 - e^-l )
Donc Y + 1 suit la loi géométrique de paramètre 1 - e^-l .
d)

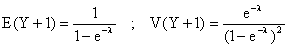
On utilise les formule E(aX + b) = aE(X) + b, V(aX + b) = a²V(X) :

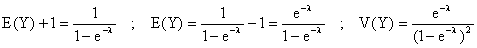
2°) a) Z = X - [X] prend ses valeurs dans [0, 1[.
b) La formule des probabilités totales utilisée avec le sce indiqué donne :


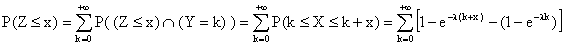
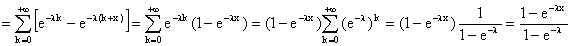
c) Z prend ses valeurs dans [0, 1[, on peut donc prendre f(x) = 0 si x n'appartient pas à [0, 1].
Si x appartient à [0, 1] :

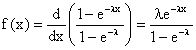
d)

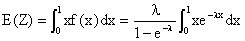
On effectue alors une intégration par parties avec u = x, v' = e^-lx, u' = 1, v = (- 1/l )e^-lx ; u et v sont de classe C¹ sur [0,1]. Tous calculs faits, on trouve :

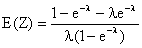
Ce résultat était prévisible dans la mesure où :

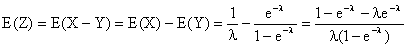
exercice 2
Tout d'abord bien comprendre le problème. Y₁ est le nombre de fois où on rencontre un "pile" isolé dans la suite des résultats, Y₂ est le nombre de fois où on rencontre une suite isolée de deux "pile", etc. On peut alors suivre son intuition, au moins pour répondre aux premières questions :
1°) En lançant n fois la pièce, on peut obtenir au plus une n-chaine de pile : P₁P₂ ... P_n. Par indépendance des lancers successifs :
P(Y_n = 1) = pⁿ, P(Y_n = 0) = 1 - pⁿ, et, puisque Y_n est une variable de Bernoulli : E(Y_n) = pⁿ.
2°) De même on obtiendra au plus une (n - 1)-chaîne de "pile" :
(Y_{n- 1} = 1) = P₁P₂ ... P_{n- 1}F_n È F₁P₂ ... P_{n- 1}. Par additivité et indépendance :
P(Y_{n- 1} = 1) = p^{n- 1}q + qp^{n- 1} = 2qp^{n- 1}, P(Y_{n- 1} = 0) = 1 -2qp^{n- 1}, E(Y_{n- 1}) = 2qp^{n- 1}.
3°) a) (X_i,k = 1) = P₁P₂ ... P_kF_k+1, donc P(X_i,k = 1) = p^kq.
b) Pour i appartenant à [[2, n - k]], (X_i,k = 1) = F_{i- 1}P_iP_i+1 ... P_i+kF_i+k+1, donc P(X_i,k = 1) = q²p^k.
c) (X_{n- k+1,k} = 1) = F_{n- k}P_{n- k+1}P_{n- k+2} ... P_{n- k+k} = F_{n- k}P_{n- k+1}P_{n- k+2} ... P_n, donc P(X_{n- k+1,k} = 1) = qp^k.
d) Une k-chaîne de "pile" commence au plus tard au (n - k + 1)-ème lancer, donc

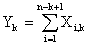
L'espérance est linéaire et les variables X_i,k sont de Bernoulli, donc :

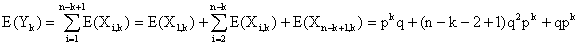
E(Y_k) = 2p^kq + q²p^k(n - k - 1).

exercice 3
1°) a) f est continue sur ]0, +¥ [ (quotient de deux fonctions continues avec le dénominateur qui ne s'annule pas) et en 0 ( car x ln(x) tend vers 0 quand x tend vers 0, donc la limite de f en 0 est égale à 0 qui est égal à f(0) ), donc f est continue sur R₊.
b) Sans l'ombre d'un doute :
x     0     1    +¥
f(x) 0 +  0  -
2°) f est continue sur [0, +¥ [, 0 appartient à [0, +¥ [, donc, pour tout x dans [0, +¥ [, F(x) est bien définie (c'est la primitive de f sur [0,+¥ [ qui s'annule en 0).
3°) F est dérivable sur R₊ et F' = f, donc g est dérivable sur R₊ comme somme de deux fonctions dérivables, et on a :

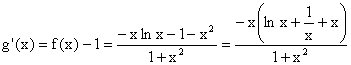
Donc, pour tout x > 0 :

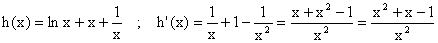
Le dénominateur est positif, les racines du polynôme du deuxième degré du numérateur sont :

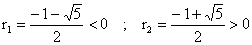
h est donc strictement décroissante sur ]0, r₂] , strictement croissante sur [r₂, +¥ [ ; h admet donc son minimum en r₂. Or ce minimum est positif :

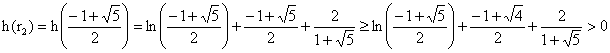
car

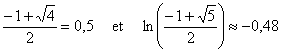
On peut donc se dispenser de l'étude de h en 0 et en +¥ , et conclure que h est positive sur ]0, +¥ [.
c) Du résultat du a), on déduit alors que g' est négatif sur ]0, +¥ [ ; g est donc strictement décroissante sur [0, +¥ [. Comme g(0) = 0, on conclut que g(x) est négatif pour tout x > 0.
4°) a) u₀ = 1 appartient à [0, 1], et si u_n (avec n appartenant à N) appartient à [0, 1], alors :

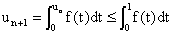
car 0 £ u_n £ 1et f est positive ou nulle sur [0, 1]. Mais

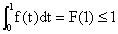
car g(1) = F(1) - 1 est négatif ou nul. On a bien obtenu u_n+1 £ 1. La conclusion en résulte, d'après le principe de récurrence.
b) g(x) = F(x) - x £ 0 sur [0, +¥ [ et u_n appartient à [0, +¥ [ pour tout n, donc F(u_n) - u_n £ 0,
u_n+1 - u_n £ 0, u_n+1 £ u_n : la suite (u_n) est décroissante.
c) (u_n) est décroissante et minorée par 0, elle est donc convergente. Sa limite est un point fixe de F, car F est continue. Or le seul point fixe de F est 0, d'après 3°)c). La suite (u_n) converge donc vers 0.

problème
partie 1
1°) a) E est l'ensemble des combinaisons linéaires des matrices I, J, K, L ; E est donc le sous-espace vectoriel de l'espace vectoriel M₄(R) engendré par la famille (I, J, K, L), donc un espace vectoriel.
b) En regardant juste la première ligne des matrices I, J, K, L :
xI + yJ + zK +tL = 0 implique x = y =z = t = 0.
La famille (I, J, K, L) est donc libre.
c) La famille (I, J, K, L) est libre et génératrice de E, c'est donc une base de E, qui est donc de dimension 4.
2°) a) La principale difficulté de cette question et de quelques-unes des suivantes est de ne pas faire tous les calculs demandés, sous peine de perdre un temps considérable à manipuler des tableaux de 16 nombres : il faut tricher un peu et repérer rapidement que chacun des produits est égal à une des matrices I, J, K, L ; il suffit alors de former la première colonne de chacun des produits pour se décider. Les calculs demandés ici seront facilités si on pense aux endomorphismes canoniquement associés à I, J, K, L. Par exemple si j est l'endomorphisme canoniquement associé à J et si (e₁,e₂,e₃,e₄) est la base canonique de R⁴, on j(e₁) = e₂, j(e₂) = e₃, donc la première colonne de J² (matrice qui représente joj) s'obtient en écrivant en colonne le vecteur e₃. Bref, on obtient :
J² = L ; K² = L ; L² = I ; J³ = K ; K³ = J
qui sont bien des éléments de E.
b) Par "sans aucun calcul matriciel", il faut comprendre "sans calculer sur les matrices explicitées".
JK= K³K = K²K² = LL = L² = I
KJ = KK³ = K²K² = LL = L² = I
KL = KK² = K³ = J
LK = K²K = K³ = J
JL = JK² = JKK = IK = K
LJ = K²J = KKJ = KI= K
appartiennent tous à E.
c) Chaque élément de E est une combinaison linéaire de I, J, K, L. Le produit de deux éléments de E est donc une combinaison linéaire des matrices I, J, K, L, J, J², JK, JL, K,KJ, K²,KL, L, LJ, LK, L². Or toutes ces matrices appartiennent à E, leur combinaison linéaire aussi. Le produit de deux matrices de E est donc une matrice de E.
3°) a) L est symétrique réelle, donc diagonalisable.
b) Sur la matrice L -l I, on effectue les opérations élémentaires

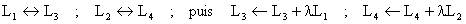
On obtient la réduite de Gauss :

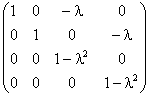
Les valeurs propres de L sont donc 1 et - 1.
Le sous-espace propre associé à la valeur propre 1 a pour équations x = z, y = t, pour base
( (1, 0, 1, 0) , (0, 1, 0, 1) )
Le sous-espace propre associé à la valeur propre - 1 a pour équations x = - z, y = - t, pour base
( (1, 0, - 1, 0) , (0, 1, 0, - 1) )
(Il est licite d'écrire les vecteurs concernés sous cette forme, en tenant compte de l'identification habituelle de M_4,1(R)à R⁴.)
4°) a) xu₁ + yu₂ + zu₃ + tu₄ = 0 est équivalent à :




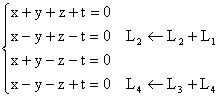
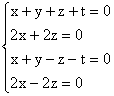
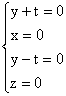
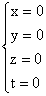
(u₁,u₂, u₃, u₄) est donc une famille libre. Comme M_4,1(R) est de dimension 4, c'est une base de M_4,1(R).
b) Là aussi, on esquisse les calculs :
Lu₁ = u₁ ;  Lu₂ = u₂ ;  Lu₃ = - u₃  ;  Lu₄ = - u₄
Et après avoir formé J + K (un damier de 0 et de 1 avec un 0 dans le coin supérieur gauche) :
(J + K)u₁ = 2u₁ ; (J + K)u₂ = - 2u₂ ; (J + K)u₃ = 0u₃ ; (J + K)u₄ = 0u₄
Ce qui montre que u₁,u₂, u₃, u₄ sont des vecteurs propres de L et de J + K.
partie 2
1°) a)

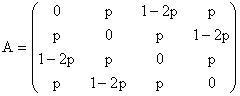
b) A = p(J + K) + (1 - 2p)L
2°) a) Au₁ = p(J + K)u₁ + (1 - 2p)Lu₁ = 2pu₁ + (1 - 2p)u₁ = u₁
Au₂ = - 2pu₂ + (1 - 2p)u₂ = (1 - 4p)u₂
Au₃ = (2p - 1)u₃
Au₄ = (2p - 1)u₄
u₁,u₂, u₃, u₄ sont donc des vecteurs propres de A pour les valeurs propres respectives 1, 1 - 4p, 2p - 1, 2p - 1. Comme (u₁,u₂, u₃, u₄) est une base de M_4,1(R), A est diagonalisable, et d'après la théorie du changement de base : A = P D P^-1 avec P obtenue en "collant" les quatre vecteurs u₁,u₂, u₃, u₄ et
D = diag(1, 1 - 4p, 2p - 1, 2p - 1)
b) P² = 4I, donc P^-1 = (1/4)I
3°) a) Le système complet d'événements est bien sûr (X_n = i), i appartenant à {1, 2, 3, 4}.
b) De C_n+1 = AC_n on déduit par récurrence, comme d'habitude : C_n = Aⁿ C₀, puis :
C_n = (P D P^-1)ⁿ C₀ = P Dⁿ P^-1 C₀ = P Dⁿ (1/4)P C₀ = (1/4)P DⁿPC₀.
C₀ est la colonne 1 0 0 0, donc PC₀ est la première colonne de P, donc

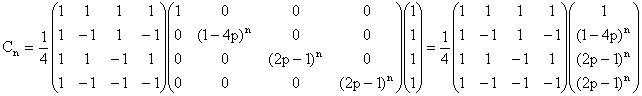
Et ya basta !
Remarquons néanmoins que p doit appartenir ]0, 1/2[ (et non pas seulement à ]0, 1[ comme le dit l'énoncé) pour que 1 - 2p appartienne à ]0, 1[. Cela assure que 1 - 4p et 2p - 1 appartiennent à ]- 1, 1[, et par conséquent la convergence en loi de (X_n) vers X variable aléatoire uniforme sur {1, 2, 3, 4}, ce qui est plutôt rassurant...