edhec 2004
voie éco ; corrigé rapide
Exercice 1
1) La fonction t ® 1/(1 + t + tn) est continue sur [0, 1] (quotient de deux fonctions continues avec le dénominateur qui ne s'annule pas), donc un existe.
2)
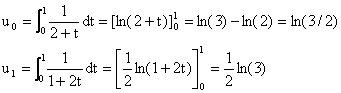
3) a. Pour tout n de N et tout t de [0, 1] :
0 £ t n+1 £ t n ; 0 < 1 + t + t n+1 £ 1 + t + t n ; donc
![]()
La suite (un) est donc croissante.
b. Pour tout n de N et tout t de [0, 1], 1/(1 + t + tn) £ 1/(1 + t), donc
![]()
Pour tout n de N, un £ ln
2.
c. La suite (un) est croissante et
majorée, elle est donc convergente.
4) a. On utilise l'expression de ln(2) trouvée précédemment, puis la linéarité de l'intégrale :
![]()
b. Pour tout t de [0, 1], (1 + t) (1 + t + tn) ³ 1, donc
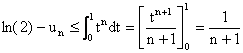
c. Du 3) b et du 4) b on déduit l'encadrement :
![]()
et par passage à la limite, étant entendu que 1/(n+1) tend vers 0 :
la suite (un) converge vers ln(2)
5) a. La fonction t ® 1/(1 + t + tn) est positive et continue sur [1, +¥[. En +¥, elles est équivalente à 1/tn, fonction dont l'intégrale sur [1, +¥[ est convergente (intégrale de Riemann, n ³ 2). L'intégrale définissant vn est donc convergente.
b. Pour tout t ³ 1, tout n ³ 2 :
![]()
Donc pour tout X ³ 1 :
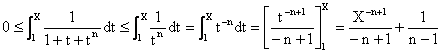
D'où le résultat, en passant à la limite (X ® +¥).
c. On en déduit par passage à la limite (n® +¥) que vn converge vers 0, et comme
![]()
on obtient finalement :
![]()
Exercice 2
1) Voilà une question qui a dû enchanter plus d'un candidat !
a. Explicitons Q(x) :
[(x 2 – x) P(x)] ' = (2x – 1)P(x) + (x2 – x)P'(x) ;
Q(x) = [(x 2 – x) P(x)] '' = 2 P(x) +(2x – 1)P'(x) + (2x – 1)P'(x) + (x2 – x) P''(x)
Q(x) = 2P(x) + 2(2x – 1)P'(x) + (x2 – x)P''(x)
* f est linéaire car pour tout P1, P2 de E et tout a de R :
f(P1
+ P2) = f(P1) + f(P2) ; f(aP1) = a f(P1).
* f est un endomorphisme de E car si P est un polynôme de degré £ 2, alors P' est un polynôme de degré £ 1, P'' est un polynôme de degré £ 0.
* Donc f est un endomorphisme de E.
b. En remplaçant P par e0, puis e1, puis e2 dans le calcul précédent :
f(e0)(x)
= 2 ;
f(e1)(x)
= 2x + 2(2x – 1) = 6x – 2 ;
f(e2)(x)
= 2x2 + 2(2x – 1)2x + (x2 – x)2 = 12x2 – 6x.
On obtient donc :
f(e0)
= 2 e0 ; f(e1) = –2 e0 + 6 e1 ; f(e3) = 6 e2 + 12 e3...
c. ... Ce qui nous donne la matrice de f dans la base B, qui est effectivement la matrice A.
d. C'est le moment de se raccrocher aux wagons, et travailler sur la matrice A donnée...
La matrice A est triangulaire sans zéros sur la diagonale, elle est donc inversible. f est donc un automorphisme de E.
2) a. La matrice A est triangulaire, les valeurs propres de A, et de f, sont donc les éléments de la diagonale de A : 2, 6, 12.
b. Pour la valeur propre 2, le système d'équations (A – 2I)X = 0 s'écrit :
–2y = 0 ; 4y – 6z = 0 ; 10z = 0.
Solution : y = z = 0, D'où E2 = Vect(e1), normal !
Pour la valeur propre 6, on obtient de même E6 = Vect(e1 – 2e2).
Et pour la valeur propre 12 : E12 = Vect(e1 – 5e2 + 5e3).
Les candidats qui ont répondu Vect(1, 0, 0), Vect(1, –2, 0), Vect(1, –5, 5) ne devraient pas être trop pénalisés....
Et on prend le temps de vérifier ses calculs, la moindre erreur rendant tout le reste de l'exercice inefficient.
3) a. f est diagonalisable, et d'après la théorie du changement de base, A = P D P–1, avec
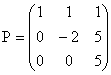
b. Par récurrence, ou An = (P D P–1) (P D P–1) ... (P D P–1) (n facteurs), donc An = P Dn P–1.
4) a. La méthode du pivot aboutit à :
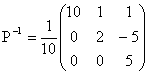
Et on prend le temps de vérifier, avant de se lancer dans des calculs inutiles...
b. On arrive tout doucettement à
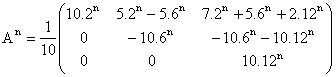
c. Bn = (1/12)nAn. En multipliant les coefficients de An par (1/12)n, on s'aperçoit que seuls les termes en 12n ne s'évanouissent pas : 10.2n/12n = 10.(2/12)n converge vers 0 par exemple. La suite (Bn) converge donc vers J, avec
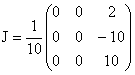
Et on constate, non sans plaisir, mais avec un peu de perplexité, que, effectivement J2 = J.
Exercice 3
1) a. ?? Je ne vois pas le problème, et une argumentation soigneuse va aboutir assez rapidement à des arguties discutables! Je propose la rédaction :
D'après la définition de Z, Z(W) est inclus dans [[0, n]].
Réciproquement, soit k un élément de [[0, n]]. Si k ³ 1, alors l'événement F1F2 ... Fk–1 Pk, de probabilité non nulle, réalise Z = k, et donc k appartient à Z(W). L'événement F1 F2 ... Fn réalise Z = 0, donc 0 Î Z(W). On a donc [[0, n]] inclus dans Z(W).
On peut donc conclure : Z(W) est égal à [[0, n]].
b. Si k ³ 1, P(Z = k) = P(F1F2 ... Fk) = (1/2)k , par indépendance des résultas successifs.
P(Z = 0) = P(F1 F2 ... Fn) = (1/2)n.
c. Attention, Z = 0 est un cas particulier :
![]()
Maintenant, on utilise l'identité géométrique, ce qui est légitime car 1/2 ¹ 1 :
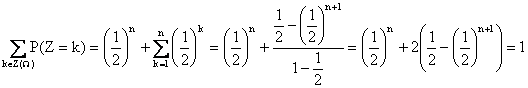
d. Merci pour ce rappel, mais l'instruction random n'est pas encore au programme... Vive le copier-coller, qui n'est malheureusement pas utilisable par les candidats :
Program EDHEC2004 ;
var
k, n, z, lancer : integer ;
Begin
Randomize ;
Readln(n) ; k : = 0 ; z : = 0 ;
Repeat
k
: = k + 1 ; lancer : = random(2) ;
If (lancer = 1) then z := k ;
until (lancer = 1 or k
= n) ;
Writeln (z) ;
end.
2) Sans y
mettre trop de soin, X(W) = [[0, n]]
car on obtient au minimum 0 boule blanche et au maximum n boules blanches, et
toutes les situations intermédiaires sont possibles, le hasard étant ce qu'il
est.
3) a. L'énoncé le dit : si Z a pris la valeur 0, alors X prend la valeur 0. Donc :
Si
1 £
i £
n, P(X = i / Z = 0)
= 0 ; P(X = 0 / Z = 0) = 1.
b. Si Z = n, on effectue n tirages dans L'urne Un qui contient n boules blanches et 0 boule noire. Donc :
Si
0 £
i £
n – 1,
P(X = i / Z = n) = 0 ; P(X = n / Z = n) = 1.
c. k appartient à { 1, 2, ..., n – 1 }.
Si k < i £ n, P(X
= i / Z = k) = 0 car on ne peut obtenir plus de k boules blanches en
k tirages.
Si 0 £
i £
k, et sachant Z = k, (X = i) est l'événement "obtenir i succès lors de k
épreuves identiques et indépendantes", la probabilité du succès à chaque
épreuve étant k/n. En effet, on effectue k tirages avec remise dans l'urne Uk
qui contient n boules dont k sont blanches.
On a donc :
![]()
4) a. Voilà une question dont la réponse est à justifier
soigneusement. Il s'agit d'utiliser la formule des probabilités totales, avec
le système complet d'événement (Z = k)0 £ k £ n :
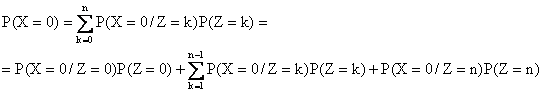
Et d'après les résultats soulignés, en remplaçant éventuellement i par 0 :
![]()
b. Même formule, avec le même système complet, mais la seule probabilité conditionnelle non nulle est P(X = n/ Z = n), qui est égale à 1... d'où le résultat, car P(Z = n) = (1/2)n.
c. Ce coup ci ne subsistent que les termes de k = 1 à k = n – 1. Pour tout i de { 1, 2, ..., n – 1 }:
![]()
5) Le morceau de bravoure :

Problème
1) a. Quand x tend vers 0+, –n/x tend vers –¥, exp(–n/x) tend vers 0, donc
fn(x) = x exp(–n/x) tend vers 0, c'est à dire vers vers fn(0) : fn est continue à droite en 0.
b. Pour x > 0 :
![]()
Donc f n est dérivable à droite en 0 le nombre dérivé à droite en 0 de fn vaut 0.(Ce nombre est noté quelquefois f 'd(0).)
2) a. Sur ]–¥, 0 [ et sur ]0, + ¥[, fn est le produit de deux fonctions dérivables, donc fn est dérivable. Pour x non nul :
![]()
fn'(x) est donc du signe de (x + n)/x, ou encore de (x + n)x, polynôme du second degré dont les racines sont 0 et –n.
fn' est donc positive sur ]–¥, –n[ et ]0, +¥[, négative sur ]–n, 0[, nulle en –n.
b. En +¥ et –¥, pas de problème, lim+¥ f = +¥, lim–¥ f = –¥.
En 0–, posons y = –n/x. y tend vers +¥ quand x tend vers 0–, x = –n/y, et
![]()
Donc f(x) tend vers –¥ quand x tend vers 0–. On obtient le tableau de variation :
|
x |
–¥ –n 0 +¥ |
|
fn'(x) |
+ 0 – || + |
|
fn(x) |
–¥ ↗ –ne ↘ –¥| 0 ↗ +¥ |
3) a. Avec e une fonction de limite nulle en 0 :
![]()
b. Posons u = n/x. u tend vers 0 quand x tend vers +¥ ou –¥, et on peut utiliser le DL précédent :
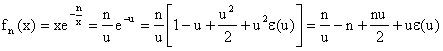
En revenant à x, c'est à dire en remplaçant u par n/x, on obtient :
![]()
Soit finalement :
![]()
c. On en déduit que la limite de fn(x) – (x – n) quand x tend vers +¥ ou –¥ est égale à 0. La droite (Dn) d'équation y = x – n est donc asymptote à (Cn). De plus fn(x) – (x – n) est du signe de n2/2x aux voisinage de +¥ et –¥. (Cn) est au dessus de (Dn) au voisinage de +¥, (Cn) est en dessous de (Dn) au voisinage de –¥.
d. Commencer par placer l'asymptote d'équation y = x – 1, puis le point (0, 0), avec sa demi-tangente horizontale, et le point (–1, –e) avec sa tangente horizontale.
4) a. Sur ]–¥, 0[, fn(x) £ –n < 1.
Sur [0, +¥[, fn est continue strictement croissante, fn(0) = 0, lim+¥ fn = +¥ ; Donc fn réalise une bijection de [0, +¥[ dans [0, +¥[, donc il existe un unique tel que fn(un) = 1.
Conclusion : il existe un réel unique un tel que fn(un) = 1, et un > 0.
b. fn(1) = e–n < 1, fn(un) = 1, fn est strictement croissante sur [0,+¥[ ; donc un > 1.
fn(un)
= 1 Û e–x/n = 1 Û e–n/x = 1/x Û –n/x = ln(1/x) Û –n/x = –ln(x) Û x ln(x) = n.
c. g(x) = x ln(x) ; g'(x) = ln(x) + 1 > 0 pour x ³ 1. g est continue strictement croissante sur [1, +¥[.g(1) = 0 et lim+¥ g = +¥, donc g réalise une bijection de [1, +¥[ sur [0,+¥[.
La bijection réciproque g–1 est strictement croissante sur [0,+¥[, g–1(0) = 1, lim+¥ g–1 = +¥.
g(un) = n donc g–1(n) = un. lim+¥ g–1 = +¥, donc limn®+¥ un = +¥.
d. un ln(un) = n, donc ln( un ln(un) ) = ln(n),
ln(un) + ln( ln(un) ) = ln(n).
ln( ln(un) ) = o+¥(ln(un)), car ln(un) ® +¥ quand n ® +¥, et limy®+¥ ln(y)/y = 0.
Donc ln(un) est équivalent à ln(n) quand n tend vers +¥.
Il ne faudrait pas en déduire hâtivement que un est équivalent à n quand n tend vers +¥ !
un ln(un) = n, donc
![]()
5) a. Pour tout n ³ 1, g(un) = n, g(un+1) = n + 1, g est strictement croissante, donc un < un+1. La suite (un) est strictement croissante.
b.
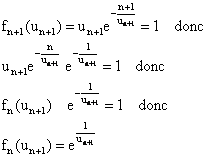
6) a. un < un+1 et pour tout t Î [un, un+1], fn(un) £ fn(t) £ fn(un+1) car fn est croissante sur [0,+¥[. On en déduit, en intégrant cette double inégalité (les bornes sont dans le bon sens) :
(un+1 – un) fn(un) £ In £ (un+1 – un) fn(un+1)
(un+1 – un) 1 £ In £ (un+1 – un) exp(1/un+1)
Et on obtient le résultat demandé en divisant par un+1 – un, qui est positif.
b. Quand n tend vers +¥, un+1 tend vers +¥, exp(1/un+1) tend vers 1, et par encadrement on obtient In équivalent à un+1 – un quand n tend vers +¥.
c. In est équivalent à un+1 – un qui est positif. Or la série de terme général un+1 – un est divergente, car sa somme partielle d'ordre N est égale à uN+1 – u1, qui tend vers +¥. La série de terme général In est donc aussi divergente.
Des questions faisables, tout de même !