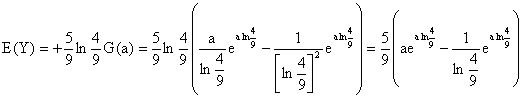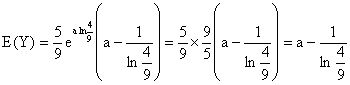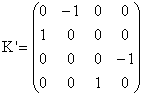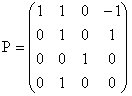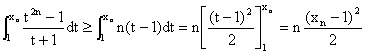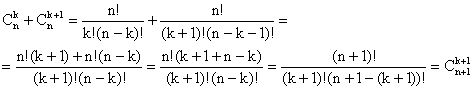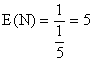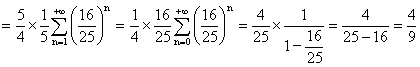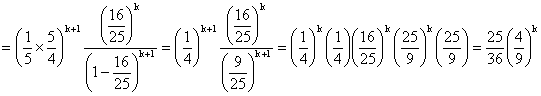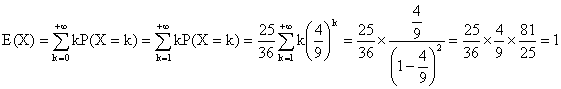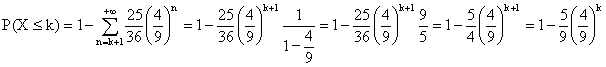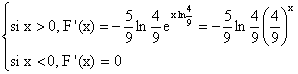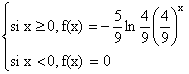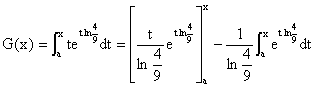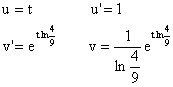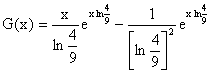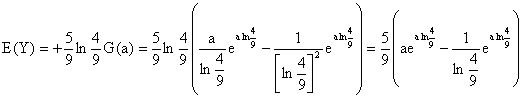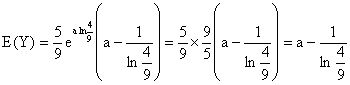exercice 1

1°) a) K² = - I.
b) K(- K) = I, donc K est inversible et K^-1 = - K.
c) Supposons que K admette une valeur propre réelle l , et soit X non nul un vecteur propre associé à la valeur propre l (ici X est une matrice-colonne à 4 éléments). Alors KX = l X, donc
K²X = KKX = Kl X = l KX = ll X = l²X.
Mais d'autre part K²X = - IX = - X. Par conséquent
l²X = - X
(l² + 1)X = 0
l² + 1 = 0
Un tel nombre (réel !) n'existe pas, par conséquent K n'admet pas de valeur propre réelle...
Malgré tout, cette méthode est plus rapide que la résolution du système habituel (K - l I)X = 0...
2°) a) M² = (aI + bK)(aI + bK) = a²I + baK + abK +b²K² = (a² - b²)I + 2abK.
- (a² + b²)I + 2aM = - (a² + b²)I + 2a(aI + bK) = - (a² + b²)I + 2a²I + 2abK) = (a² - b²)I + 2abK.
Donc M² = - (a² + b²)I + 2aM.
b) On en déduit :
M² - 2aM = - (a² + b²)I.
M(M - 2aI) = - (a² + b²)I.
(a, b) est différent de 0, donc a² + b² est différent de 0, donc

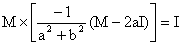
Donc M est inversible, et

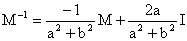
c) La matrice proposée est :

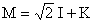
Son inverse est donc :

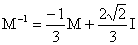
3°) a) x v₁ + y v₂ + z v₃ + t v₄ est égal à 0 ssi :
x (1, 0, 0, 0) + y (1, 1, 0, 1) + z (0, 0, 1, 0) + t (- 1, 1, 0, 0) = 0
(On va chercher les valeurs de v₂ = f(e₁) et v₄ = f(e₃) respectivement à la première et troisième colonne de K)
x + y - t = 0, y + t = 0, z = 0, y = 0
x = y = z = t = 0
La famille C est donc libre ; comme R⁴ est de dimension 4, ceci prouve que C est une base de R⁴.
b) f(v₁) = f(e₁) = v₂
f(v₂) = f(f(e₁)) = fof(e₁) = - e₁ = - v₁ : en effet, la matrice de fof dans la base canonique est K², et K² = - I.
f(v₃) = f(e₃) = v₄
f(v₄) = f(f(e₃)) = - e₃
Par définition de K', on a donc :

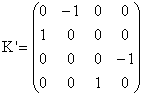
c) v₁ = (1, 0, 0, 0), v₂ = (1, 1, 0, 1), v₃ = (0, 0, 1, 0), v₄ = (- 1, 1, 0, 0), donc

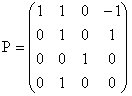
d) D'après la théorie du changement de base : K' = P-¹KP.

exercice 2
I. 1°)


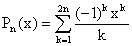
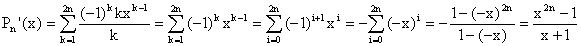
On a utlisé l'identité géométrique, ce qui est licite car - x est différent de 1.
2°) Sur [0, +¥ [, x + 1 est positif, et
x²ⁿ - 1 ³ 0 Û x²ⁿ ³ 1 Û x ³ 1
P_n est donc strictement décroissante sur [0, 1], strictement croissante sur [1, +¥ [. P_n(0) = 0 et P_n(x) est équivalent en +¥ à son terme de plus haut degré x²ⁿ, donc P_n(x) tend vers +¥ quand x tend vers +¥ .
3°) P_n(0) = 0 et P_n est strictement décroissante sur [0, 1], donc P_n(1) < 0.
4°) a)


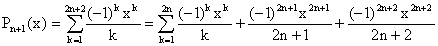
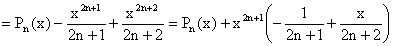
b) Pour n = 1 : P₁(x) = - x + x²/2, P₁(2) = 0 ³ 0.
Si l'entier n est tel que P_n(2) ³ 0, alors d'après a) :

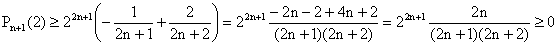
La conclusion en résulte, d'après le principe de récurrence.
5°) Sur l'intervalle [1, +¥ [, P_n est continue et strictement croissante, P_n(1) < 0 et P_n a pour limite +¥ en +¥ . Par conséquent l'équation P_n(x) = 0 d'inconnue x appartenant à [1, +¥ [ admet une unique solution x_n. De plus P_n(1) < 0 et P_n(2) ³ 0, donc 1 < x_n £ 2.
6°) Il n'y a pas d'autre choix que d'utiliser la méthode de dichotomie :
program escl ;
var a, b, c : real ;
function P(x :real) : real ;
begin P := - x + x*x/2 - x*x*x/3 + x*x*x*x/4 ; end ;
BEGIN
a:= 1 ; b := 2 ;
repeat c:= (a + b)/2 ; if P(c) < 0 then a:= c else b:= c ; until (b - a < 0.001) ;
writeln(c) ;
END.
II. 1°) D'après I 1°), P_n est une primitive de la fonction sous le signe intégrale, donc :

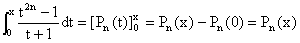
2°) On utilise la définition de x_n, le 1°), puis la relation de Chasles :

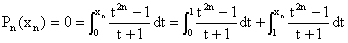
On a donc :

3°) Soit g(t) = t²ⁿ - 1 - n(t² - 1) ; g'(t) = 2nt^{2n- 1} - 2nt = 2nt(t²ⁿ - 1) > 0 sur ]1, +¥ [. g est donc strictement croissante sur [1, +¥ [. g(1) = 0, donc g est positive ou nulle sur [1, +¥ [, donc, sur [1, +¥ [ :
t²ⁿ - 1 ³ n(t² - 1)
4°) x_n appartient à [1, +¥ [, donc sur [1, x_n], on a :
t²ⁿ - 1 ³ n(t² - 1)


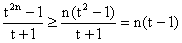
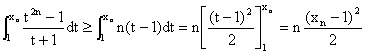
On a par conséquent :

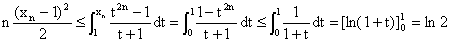
D'où le résultat voulu en prenant la racine carrée de ces deux nombres, car x_n - 1 > 0.
5°) Par encadrement : la suite (x_n - 1) converge vers 0, et donc la suite (x_n) converge vers 1.

exercice 3
1°) a) Pour tout x appartenant à [0, 1[ :

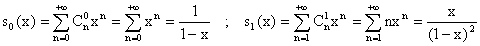
b) Il s'agit de démontrer la formule de Pascal.

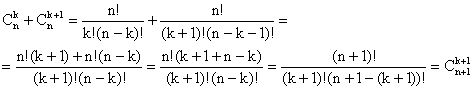
On peut préférer une démonstration combinatoire :
le nombre de parties à k + 1 éléments d'un ensemble à n + 1 éléments E = {a₁, a₂, ... , a_n, b} est :

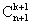
Parmi ces parties, certaines contiennent b, elles sont au nombre de C_n^k. Les autres ne contiennent pas b, elles sont au nombre de C_n^k+1. La conclusion en résulte.
c) Après ces hors-d'œuvre, une question qui demande du soin ; pour k entier et x dans [0, 1[, le nombre xs_k(x) + xs_k+1(x) est successivement égal à :





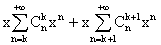
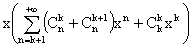
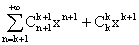
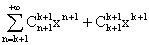
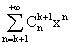
s_k+1(x)
Ne pas perdre de vue que c'est k qui est fixé, et n qui varie...
d) La propriété à établir est vraie pour k = 0 et k = 1 d'après a). Supposons la vraie pour k, avec k appartenant à N. Alors, d'après c) :
(1 - x)s_k+1(x) = xs_k(x)

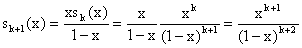
La conclusion en résulte, par récurrence.
3°) a) N prend ses valeurs dans N*, et, pour tout n appartenant à N*, P(N = n) = (4/5)^{n- 1}(1/5) par indépendance des tirages successifs. N suit donc la loi géométrique de paramètre 1/5 ,et

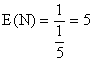
b) Sachant N = n, on a X = k ssi on obtient k succès (obtenir la boule noire) au cours de n épreuves identiques et indépendantes. Par conséquent :

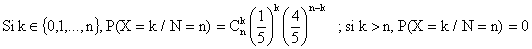
c) On utilise la formule des probabilités totales avec le système complet d'événements (N = n), n appartenant à N* :


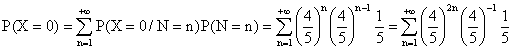
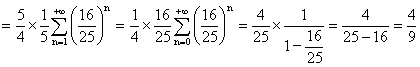
d) Même argument, pour tout k appartenant à N* :


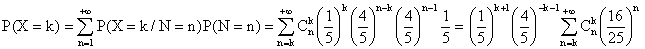
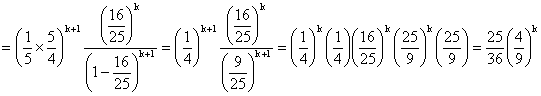
e) Sous réserve de convergence absolue :

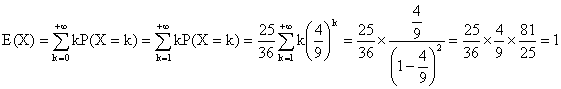
f) Pour tout k appartenant à N, P(X £ k) = 1 - P(X > k) = 1 - P(X ³ k + 1), donc

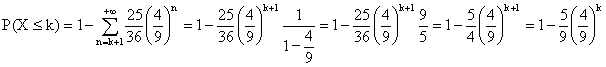
3°) a) Montrons d'abord que F est continue en a. La limite à gauche de F en a est égale à 0, la limite à droite de F en a est égale à F(a), or F(a) est égale à 0, en effet :

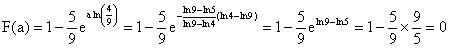
Les limites à droite et à gauche de F en a sont toutes deux égales à F(a), donc F est continue en a.
* F est continue ]-¥ , a[ (fonction nulle), sur ]a, +¥ [ (somme de deux fonctions continues), et en a, donc F est continue sur R.
* F est de classe C¹ sur ]-¥ , a[ (fonction nulle) et sur ]a, +¥ [ (somme de deux fonctions de classe C¹).
* La limite de F en -¥ est 0, la limite de F en +¥ est 1, car

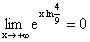
* Pour tout x appartenant à ]a, +¥ [ :

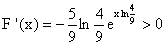
F est donc croissante sur R.
* F est donc la fonction de répartition d'une variable aléatoire à densité Y.
b) On a :

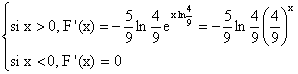
Y admet donc pour densité f telle que :

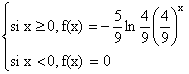
c) Une primitive G de g est :

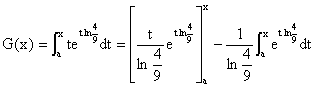
On a effectué une intégration par parties avec

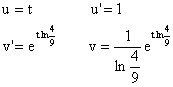
u et v sont de classe C¹ sur R. On obtient donc la sympathique expression : (la constante induite par a n'a pas d'importance, une primitive de f est définie à une constante près)

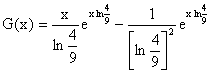
d) Sous réserve de convergence :

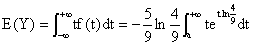
La convergence est assurée car f est continue sur [a, +¥ [ et G(x) tend vers 0 quand x tend vers +¥ .On trouve :