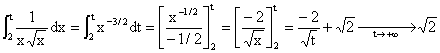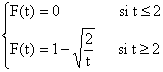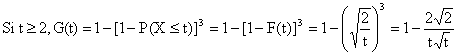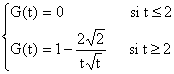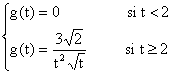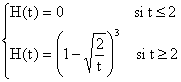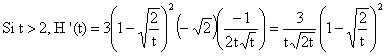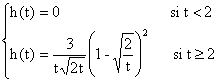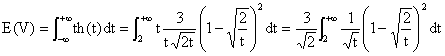Première partie
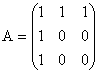
1°)
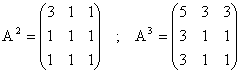
A2 + 2A = ... A3, donc A3 = A2 + 2A.
2°) A et A2 ne sont pas colinéaires (leurs composantes ne sont pas proportionnelles), donc (A, A2) est une famille libre de M3(R).
3°) On va établir le résultat proposé par récurrence, en portant une particulière attention à l'unicité...
La propriété à établir est vraie pour n = 1, car A1 = A = 1´ A + 0´ A2. A s'exprime donc comme combinaison linéaire de A et A2, et cette combinaison linéaire est unique, car la famille (A, A2) est libre. (En effet, A appartient au sev engendré par A, A2, et (A, A2) est une base de ce sev.)
On a donc
a1 = 1 ; b1 = 0
Supposons la propriété vraie pour n fixé dans N* : il existe un couple unique (an, bn) tel que An = anA + bnA2. Alors :
An+1 = An ´A = (anA + bnA2) ´ A = anA2 + bnA3 = anA2 + bn(A2 + 2A) = 2bnA + (an + bn)A2
La propriété est donc établie pour n + 1 : il existe un couple unique (an+1, bn+1) tel que An+1 = an+1A + bn+1A2, et on a :
an+1 =2bn ; bn+1 = an + bn
La conclusion en résulte, par récurrence.
4°)
program eml03;
var a, b, aux : real ; i, n : integer ;
BEGIN
readln(n) ; a : = 1 ; b : = 0 ;
writeln(1, a, b) ;
for i : = 2 to n do
begin aux : = a ; a : = 2*b ; b : = aux + b ; writeln(i, a, b) ; end ;
END.
5°) a) an+1 = 2bn et bn+1 = an + bn, donc
an+2 = 2bn+1 = 2(an + bn) = 2an + 2bn = 2an + an+1 = an+1 + 2an
b) La suite (an) est donc une suite linéaire récurrente à deux termes, d'équation caractéristique r2 = r + 2 ; les solutions de cette équation sont - 1 et 2, on a donc, pour tout n ³ 1 :
an = a (- 1)n + b 2n
avec
a1 = 1 = -a + 2b
a2 = 0 = a + 4b
(a2 est égal à 0 car A2 = 0´ A + 1´ A2)
En résolvant ce système, on trouve a = 1/6, b = - 2/3, ce qui permet d'écrire, pour n ³ 1 :
an = (- 2/3)(- 1)n +(1/6)2n
Pour bn, on a an+1 = 2bn, donc bn = (1/2)an+1, soit
bn = (1/3)(- 1)n +(1/6)2n
et on prend le temps de vérifier que ça marche pour n = 1 et n = 2, histoire d'éliminer de possibles petites erreurs...
c) An = anA + bnA2 avec an et bn comme trouvés ci-dessus.
deuxième partie A = Mat(f, (e1, e2, e3))
1°) Im(f) est engendré par les vecteur-colonne de A ; on en extrait la famille libre ( (1, 1, 1) , (1, 0, 0) ), qui est une base de Im(f), qui est de dimension 2.
2°) a) Oui, f est diagonalisable, car sa matrice A est symétrique réelle.
b) Non, f n'est pas bijectif, car f n'est pas surjectif, car Im(f) n'est pas égal à R3.
3°) On résout (f - l Id)(u) = 0 (ou A -l I) = 0...) ; Les manipulations élémentaires
L1 « L3 ; L2¬ L2 - L1 et L3 ¬ L3- (1 - l )L1 ; L2 « L3 ; L3 ¬ L3 + l L2
sur la matrice A - l I conduisent à la matrice
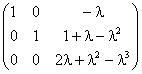
2l + l2- l3 = 0 ssi l = 0 ou l = - 1 ou l = 2, qui sont donc les trois valeurs propres de f.
Pour les sous-espaces propres, on jette un coup d'oeil aux questions qui suivent :
Pour l = - 1, on a x + z = 0, y - z = 0 ; sous-espace de base (- 1, 1, 1) ;
Pour l = 0, on a x = 0, y + z = 0 ; sous-espace de base (0, - 1, 1) ;
Pour l = 2, on a x - 2z = 0, y - z = 0 ; sous-espace de base (2, 1, 1) .
Là aussi, on prend le temps d'éliminer d'éventuelles menues erreurs...
4°) A est diagonalisable, et d'après la théorie du changement de base, A = P D P-1, avec :
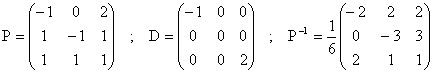
Ce dernier résultat (P-1) obtenu avec la méthode du pivot, ou toute autre méthode acceptable. On peut s'épargner ce calcul si on n'est pas absolument sûr de l'expression de P et D, qui doivent vérifier les contraintes de l'énoncé...
5°) Posons M = PXP-1 ; l'équation proposée, AM + MA = 0, est équivalente successivement à :
(PDP-1)(PXP-1) + (PDP-1)(PXP-1) = 0
PDXP-1 + PXDP-1 = 0
P(DX + XD)P-1 = 0
DX + XD = 0
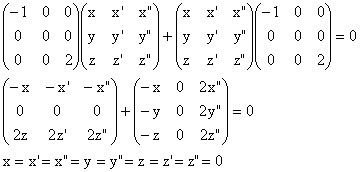
Ne subsiste que y'... L'ensemble des matrices M telles AM + MA = 0 est donc l'ensemble des matrices x P M2,2 P-1, avec x appartenant à R, et M2,2 la matrice dont tous les termes sont nuls, sauf celui en deuxième ligne et deuxième colonne, qui est égal à 1.