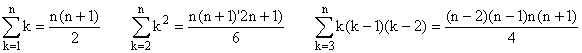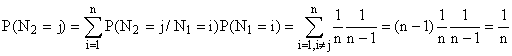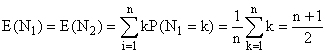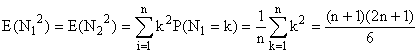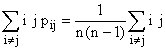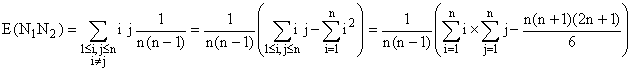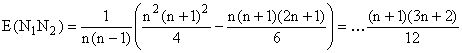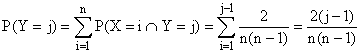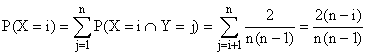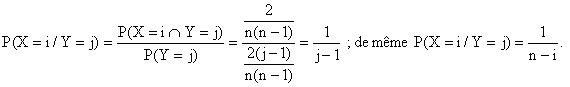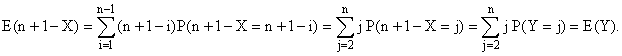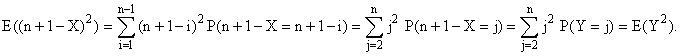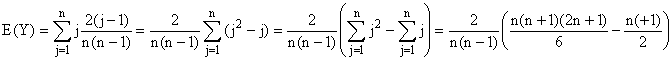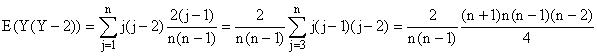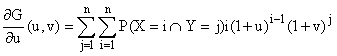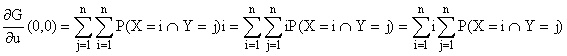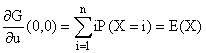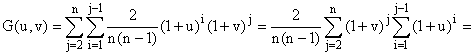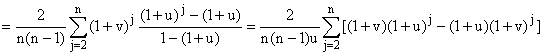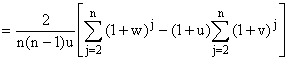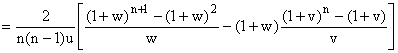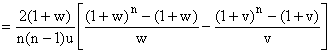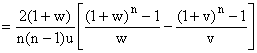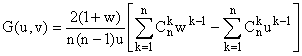Partie I

1°) a) Cov(l X+Y, l X+Y) = V(l X+Y). On utilise la linéarité de l'espérance :
Cov(l X+Y, l X+Y) = E( (l X+Y)² ) - ( E(l X+Y) )² = E(l²X² + 2l XY + Y²) - [l E(X) + E(Y)]²
= l² E(X²) + 2l E(XY) + E(Y²) - [l² E(X)² + 2l E(X)E(Y) + E(Y)²]
= l²[E(X²) - E(X)²] +2l [E(XY)- E(X)E(Y)] + E(Y)² _-E(Y)²
= l²V(X) + 2l Cov(X,Y) + V(Y) = V(l X+Y) = P(l ).
b) Pour tout réel l , V(l X+Y) est positif ou nul, par conséquent le discriminant D du poynôme du second degré P(l ) est négatif ou nul : 4[Cov(X,Y)]² - 4V(X)V(Y) £ 0, [Cov(X,Y)]² £ V(X)V(Y),d'où le résultat en divisant par V(X)V(Y) qui est > 0. Il y a égalité ssi D = 0, ssi l'équation P(l ) = 0 admet une une solution, ssi il existe l tel que V(l X+Y) = 0, ssi l X+Y = Cte, Y =l X + Cte avec probabilité 1, ssi X et Y sont corrélées...

2°) a) On se souvient que (et l'énoncé nous souffle la bonne réponse !) :

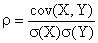
D'après le 1°) b), r² £ 1, donc r Î [- 1, 1], et r est égal à - 1 ou +1 ssi r² = 1, ssi D = 0, ssi X et Y sont corrélées.
b) Si X et Y sont indépendantes, alors Cov(X,Y) = 0, donc r = 0...
c) Avec X qui suit la loi normale centrée réduite et Y = X², on a :
E(X) = 0 ; V(X) = 1 ; E(Y) = E(X²) = V(X) + E(X)² = 1.
V(Y) = E(Y²) - E(Y)² = E(X⁴) - 1 et c'est parti :

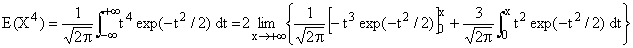
(intégration par parties avec u = t³, v' = t exp(- t²/2), u' = 3t², v = - exp(- t²/2) ; u, v Î C¹(R).)
La partie toute intégrée tend vers 0 et l'intégrale tend vers 3E(X²) = 3, donc E(X⁴) = 3, V(Y) = 2.
Cov(X, Y) =Cov(X, X²) = E(X³) - E(X)E(X²) = 0 car E(X) = 0 et E(X³) = 0 (intégrale convergente d'une fonction impaire).
Le coefficient de corrélation de X et Y est donc nul, mais X et Y = X² ne sont pas indépendantes : par exemple P(X ³ 1 Ç X² £ 1) = 0, alors que P(X ³ 1) P(X² £ 1) ¹ 0. Ceci prouve que la réciproque de la proposition : (X et Y indépendantes Þ r (X, Y) = 0) est fausse.

Partie II

1°) a) * Avec n = 0, la propriété est vraie : 0 £ q £ 0, donc q = 0, et :

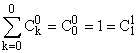
* Supposons la propriété vraie à l'ordre n : pour tout q tel que 0 £ q £ n,
.
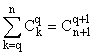Soit alors q tel que 0 £ q £ n + 1. On a :
– d'une part, si 0 £ q £ n, alors

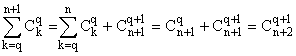
– d'autre part, si q = n + 1, alors

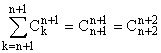
La propriété est donc vraie à l'ordre n.
* La propriété est donc vraie pour tout n.
b) Avec q = 1,
.
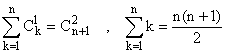Avec q = 2,


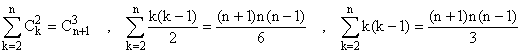
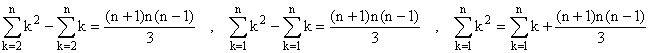
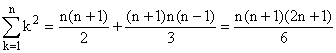
Avec q = 3,
.
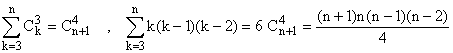On récapitule les résultats qui vont servir :

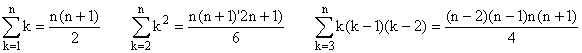
2°) a) Pour 1 £ i £ n, P(N₁ = i) = 1/n.
Pour 1 £ j £ n, j ¹ i, P(N₂ = j / N₁ = i) = 1/(n- 1). Formule des probabilités totales :

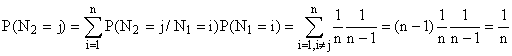
N₁ et N₂ suivent la même loi, la loi uniforme sur {1,2, ... , n}..
b)



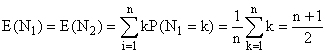
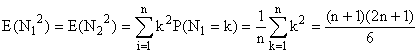
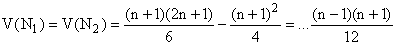
Les ... sont à la place des calculs élémentaires qu'il faut absolument savoir faire : réduction au même dénominateur (12), factorisation du numérateur, simplification...
c) Avec les notations standard, p_ii = 0 et si i ¹ j, p_ij = P(N₁ = i) P(N₂ = j / N₁ = i) = 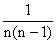. Pour le calcul de E(N₁N₂), rusons un peu. Il s'agit de calculer

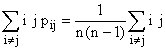
Il semble donc qu'il faille calculer la somme des éléments de la "table de Pythagore" de rang n, puis retirer les éléments de la diagonale... En explicitant :

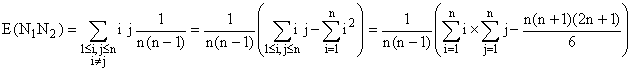
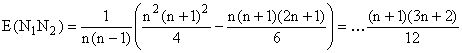
Cov (N₁N₂) = E(N₁N₂) - E(N₁)E(N₂) = (n + 1)(3n + 2)/12 - (n + 1)²/4 = ... -(n + 1)/12
r (N₁, N₂) = ... - 1/(n- 1).
d) V(N₁ + N₂) = V(N₁) + V(N₂) + 2Cov(N₁, N₂) = ... (n + 1)(n - 2)/6

3°) a) Avec 1 £ i < j £ n, (X = i Ç Y = j) = (N₁ = i Ç N₂ = j) È (N₁ = j Ç N₂ = i). Par additivité, on a :
Avec 1 £ i < j £ n, P(X = i Ç Y = j) =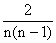 
Dans tous les autres cas, P(X = i Ç Y = j) = 0, car X < Y.
b) Pour 2 £ j £ n,

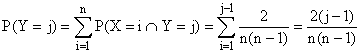
Valable aussi avec j = 1. Pour 1 £ i £ n- 1 :

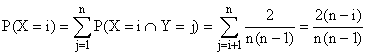
Valable aussi avec i = n. (Ce qui est normal dans l'un et l'autre cas, car les formules utilisées restent correctes, mais cela mérite d'être vérifié : si cela ne marche pas, il y a une erreur que l'on peut prendre le temps de corriger ; si cela marche, c'est comme même bon signe...; - )
c) Toujours avec 1 £ i < j £ n :

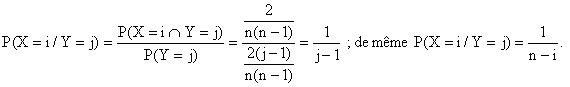
X /Y = j suit la loi uniforme sur {1, ... , j -1} . Y /X = i suit la loi uniforme sur { i + 1, ... , n}.
d) P(n + 1 - X = j) =P(X = n + 1 - j) = .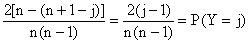
D'après la définition de l'espérance (et non pas d'après le théorème de transfert) :

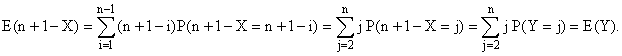
(On a effectué le changement d'indice j = n + 1 - i.) De même pour E( (n + 1 - X)² ) :

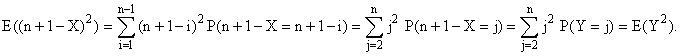
On a donc : E(n + 1 - X) = E(Y) ; V(n + 1 - X) = V(Y).
Mais E(n + 1 - X) = n + 1 - E(X) et V(n + 1 - X) = V(Y), donc :
E(X) = n + 1 - E(Y) ; V(X) = V(Y).

4°) a) D'après l'expression de P(Y = j) trouvée en 3°) b), valable pour 1 £ j £ n , on a :

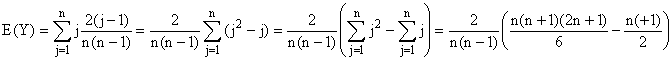
E(Y) = ... 2(n+1)/3 , et E(X) = n + 1 - 2(n+1)/3 = (n+1)/3.

b)

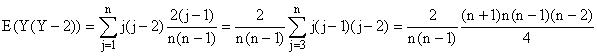
Donc E( Y(Y - 2) ) = (n+1)(n- 2)/2, E(Y²) - 2E(Y) = (n+1)(n- 2)/2,
E(Y²) = (n+1)(n- 2)/2 - 2E(Y) = ... (n+1)(3n+2)/6,
V(Y) = E(Y²) - E(Y)² = ... (n+1)(n- 2)/18. Loufoque !

5°) a) La somme du plus grand nombre et du plus petit nombre obtenus est égale à la somme du premier et du deuxième nombre obtenus, donc X + Y = N₁ + N₂. On en déduit que :
V(X + Y) = V(N₁ + N₂) = (n+1)(n- 2)/6.
Cov(X, Y) = (1/2) [V(X + Y) - V(X) - V(Y)] = ... (n+1)(n- 2)/36
b) Et pour finir, r (X, Y) = ... 1/2 (interprétation ???).
6°) a)



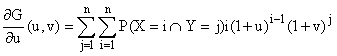
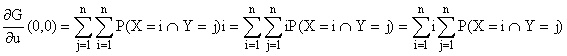
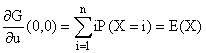
De même pour (¶ G/¶ v)(0,0) = E(Y).
A vue de nez, ou en esquissant le calcul :

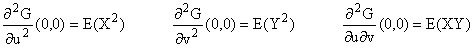
Notons que la connaissance de la loi du couple (X, Y) est ici inutile...
b) ... Ce qui n'est pas le cas pour la suite.
Avec 1 £ i < j £ n, P(X = i Ç Y = j) = 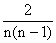 ; sinon P(X = i Ç Y = j) = 0. Donc :






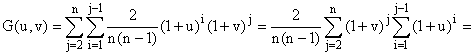
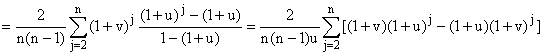
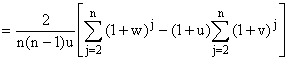
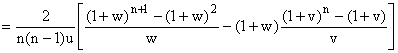
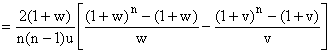
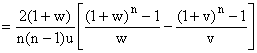
En développant (1 + w)ⁿ et (1 + u)ⁿ, on trouve :

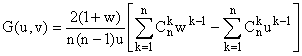
Et je ne vois ce qu'on peut faire de mieux...
c) Certes, de w = u + v + uv, on déduit sans difficultés ¶ w/¶ u = 1 + v, ¶ w/¶ v = 1 + u... Il s'agit maintenant de calculer p, q, r, s, t avec la sympathique expression trouvée... Notons qu'il s'agit maintenant d'une fonction de trois variables u, v, w. Appelons la F(u,v, w) :
G(u, v) = F(u, v, w).
Le programme est clair : pour une fonction f (x, y)de deux variables, la formule

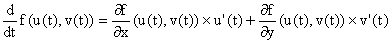
est connue. Il est donc demandé aux candidats d'extrapoler ceci de la manière suivante :

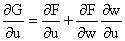
et de faire les calculs de p, q, r, s et t... Il semble raisonnable de s'arrêter là, nous avons bien travaillé...
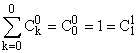
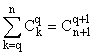
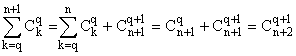
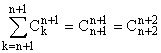
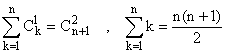
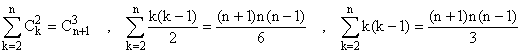
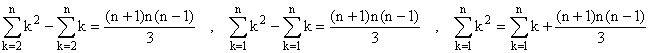
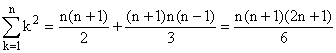
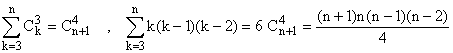