Equations du premier degré à une inconnue

Théorème. Soit a, b deux nombres réels. Soit S = {x Î R ; ax + b = 0}.

* Si a = 0 et b ¹ 0, S est l'ensemble vide.
* Si a = 0 et b = 0, S = R.

Dem : Dans tous les cas : ax + b = 0 Û ax + b - b = 0 - b Û ax = - b.
(On "passe" le b de l'autre coté de l'égalité, mais il ne s'agit pas d'un tour de passe-passe...)
* Supposons a différent de 0. Alors :

D'où la conclusion dans ce cas-là.
* Supposons a = 0. Alors l'équation ax + b = 0 s'écrit 0 = b, ou, si l'on préfère : 0x = b.
Si b est différent de 0, il est clair que l'on pourra remplacer x par ce qu'on voudra, l'égalité proposée ne sera jamais vraie.
Si b est égal à 0, au contraire...

Une conséquence pratique très importante :

L'équation dans R : ax = b admet une solution unique ssi a ¹ 0.

* Application aux systèmes linéaires :
Un système triangulaire admet une unique solution ssi les éléments de la diagonale sont tous non nuls.

Exemple : résoudre le système linéaire :

on discutera suivant la valeur du paramètre a .

Réponse :

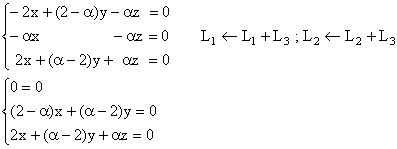
On a obtenu un système triangulaire (inférieur) ; Un des termes de la diagonale est nul, ce système n'admet donc jamais de solution unique. Comme (0, 0, 0) est toujours solution, le système admet toujours une solution non nulle. On obtient :
* Si a ¹ 0, a ¹ 2, l'ensemble S(a ) des solutions est le sev de R³ de base ( (1, 1, - 1) ) ;
* S(0) a pour base ( (1, 1, 0) , (1, 1, 1) ) (équation x = y) ;
* S(2) a pour base ( (1, 1, - 1) , (1, 0, - 1) ) (équation x + z = 0).
 

Inéquations du premier degré à une inconnue

* Signe de P₁(x) = ax + b : Si a = 0, P₁(x) = b pour tout x, donc du signe de b...
si a ¹ 0, P₁(x) admet une unique racine, - b/a , et on a :

x	-¥                     - b/a                            +¥
ax + b	signe(- a)       0            signe(a)

 

Equations et inéquations du second degré (strictement) à une inconnue

· Soit le polynôme réel de degré 2, P₂(x) = ax² + bx +c, a ¹ 0. Tout découle de ce calcul :

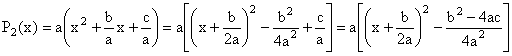
Soit D = b² - 4ac.
* Si D < 0, P₂(x) n'est jamais nul (le crochet est la somme d'un nombre positif et d'un nombre positif ou nul), P₂(x) est du signe de a pour tout x, et P₂(x) n'est pas factorisable dans R[x].
* Si D = 0, P₂(x) = 0 pour x = - b/(2a), du signe de a sinon, P₂(x) est factorisable dans R[x], et - b/(2a) est racine double de P₂(x) .
* Si D > 0, on factorise le crochet qui est de la forme A² - B². Les deux facteurs sont du premier degré, P(x) admet deux racines (distinctes) x₁ et x₂ avec :

P₂(x) est factorisable dans R[x] : P₂(x) = a(x - x₁)(x - x₂).
P₂(x) est nul en x₁ et x₂, du signe de a à l'extérieur des racines, du signe de - a à l'intérieur.

· Somme et produit des racines : Supposons que P₂(x) ait au moins une racine. En développant le second membre dans l'égalité :
ax² + bx + c = a(x - x₁)(x - x₂)
et en identifiant, on obtient :
Quand elles existent :
* La somme des racines de ax² + bx + c est égale à - b/a.
* Le produit des racines de ax² + bx + c est égal à c/a.

Application :
Soit l'équation ax² + bx + c = 0, a ¹ 0.
* si a + b + c = 0, les racines de ax² + bx + c sont 1 et c/a.
* si a - b + c = 0, les racines de ax² + bx + c sont - 1 et - c/a.

· Exercices. Les formules de résolution de l'équation du second degré sont relativement sophistiquées. On évite de les employer quand on peut faire plus simplement... C'est le cas pour :
* une équation "incomplète" : ax² + c = 0 (factoriser quand c'est possible, ou isoler x²) , ax² + bx = 0 (factoriser par x) ;
* une équation avec "racine évidente" : 1 (l'autre est c/a), - 1 (l'autre est - c/a).
* les identités remarquables (en factorisant)
On s'appliquera à résoudre les équations et inéquations suivantes sans utiliser le discriminant :
a) x² + 4 = 0
b) x² - 4 = 0
c) 7 - 9x² = 0
d) x² + 12x = 0
e) - x² +5x + 6 = 0
f) x² + 6x + 9 £ 0
g) x² £ 0
h) x² ³ 9
i) x² - 1 £ 1

Rep :
a) pas de solution (dans R)    b) 2 et - 2       c) Ö 7/3 et -Ö 7/3       d) 0 et - 12
e) - 1 et 6                             f) - 3               g) 0                            h) ]-¥ , 3] È [3, +¥ [        i) [- 2, 2]