Irrationnel signifie : qui n'est pas rationnel. Pour prouver qu'un nombre n'est pas rationnel, il faut donc procéder par l'absurde, puisqu' on ne sait rien, dans un premier temps, sur les nombres irrationnels.
Un nombre rationnel est le quotient de deux nombres entiers.

Supposons donc que :

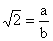
avec a et b deux entiers.
Nous allons aboutir à une contradiction.
D'une part :
a et b ne sont pas tous les deux des nombres pairs.
Sinon, on divise a et b tous les deux par 2, ... , jusqu'à obtenir une fraction où le numérateur et le dénominateur ne sont pas tous les deux divisibles par 2 ! (rappel : un nombre pair est un nombre divisible par 2. Exemple : 0 est un nombre pair, car zéro divisé par deux égale zéro, reste zéro !)
D'autre part :
a est un nombre pair.
En effet :

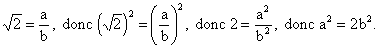
a² est donc un nombre pair.
Or : Si a est pair, alors a² est pair (si a = 2n, alors a² = 4n² est divisible par 2.)
Si a est impair, alors a² est impair (si a = 2n + 1, alors a² = 4n² + 4n + 1 n'est pas divisible par 2.)
Donc : a est un nombre pair.
Et enfin :
b est un nombre pair.
En effet , on vient de voir que que a est un nombre pair, c'est à dire que a est le double d'un nombre entier a' : a = 2a'.
Donc a² = (2a')² = 4a' ².
Comme a² = 2b², il en résulte que 4a' ² = 2b², puis (en divisant par 2 !) b² = 2a' ².
b² est donc un nombre pair.
Et comme précédemment : b est un nombre pair.
On a donc obtenu :

a et b ne sont pas tous les deux des nombres pairs.
a est un nombre pair.
b est un nombre pair.

Quelque chose ne va pas...
Et la seule chose qui n'aille pas, c'est l'hypothèse que nous avons faite, à savoir : Ö 2 est un nombre rationnel.
Donc il s'agit d'un nombre irrationnel...
Mais si il est irrationnel, où est-il ? L'usage exclusif que nous avons fait des nombres rationnels (et les nombres rationnels ne sont que les rapports de nombres entiers...) semble nous interdire de sortir de cet univers.
Ou alors c'est que Ö2 n'existe pas.
Ben si il existe : Ö2 est la longueur de la diagonale d'un carré de coté 1, d'après le théorème de Pythagore....

Pour la prochaine fois :

- Prouver que Ö 5 est un nombre irrationnel. En déduire que le nombre d'or, égal à

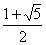
est un nombre irrationnel (indication : procéder par l'absurde !).

- Plus généralement, montrer que si n est un nombre entier naturel, alors Ön est un nombre irrationnel, à moins que n ne soit le carré d'un entier naturel, auquel cas Ön est un entier naturel. Montrer que si x est un nombre irrationnel et a et b deux nombres rationnels, alors ax + b est un nombre irrationnel.

Ainsi devant nos yeux éblouis se multiplient les nombres irrationnels.