fonctions polynômes
I. définitions
Une fonction polynôme (ou : polynôme) est
une fonction P de R dans R définie par :

où a0, a1, ... , an sont des
réels.
Le plus grand entier n tel que an est différent de
0 est le degré du polynôme. On note d°(P) = n.
Si tous les ai sont nuls, P est la fonction nulle, et on convient
que son degré est -¥ .
a est une racine du polynôme
P ssi P(a ) = 0.
II. exemples
* la fonction nulle : P(x) = 0 pour tout x. d°(P) = -¥
.
* les polynômes de degré £
0 : P(x) = a0 : ce sont les fonctions constantes.
* les polynômes de degré £
1 : P(x) = a0 + a1x. Ce sont les fonctions affines,
leur représentation graphique est une droite.
* les polynômes de degré 2 : P(x) = a0 + a1x
+ a2x2, avec a2 non nul. Représentation
graphique : une parabole, admettant deux branches paraboliques de
direction (Oy)...
* les polynômes de degré 3 : P(x) = a0 + a1x
+ a2x2 + a3x3, avec a3
non nul.
* e.t.c.
III. propriétés
* A l'infini, un polynôme est équivalent à son terme
de plus haut degré.
* Tout polynôme de degré impair admet au moins une racine
(dans R) : appliquer le théorème des valeurs intermédiaires,
après avoir étudié les limites de P a l'infini. Ce
n'est pas le cas des polynômes de degré pair : x2
+ 1 n'a pas de racine (dans R).
* Si P et Q sont des polynômes, alors PQ et P + Q sont des polynômes,
et :
d°(PQ) = d°(P) + d°(Q) ; d°(P +
Q) £ max ( d°(P), d°(Q) ).
* Le théorème
fondamental est le suivant :
P(x) est factorisable
par x - a ssi a
est une racine de P
Ce qui signifie :
P(x) = (x
- a )Q(x) avec Q polynôme non nul
Û
P(a ) = 0
Dans un sens (Þ ) c'est évident.
Dans l'autre, on admet...
Conséquences :
1°) Un polynôme de degré n ³
1 admet au plus n racines
En effet, soit P un polynôme admettant p racines (distinctes)
a1,
a2,
... , ap, avec p > n. Alors, d'après
le théorème fondamental :
P(x) = (x - a1)(x
- a2) ... (x - ap)Q(x)
avec Q non nul. Le degré de P est alors supérieur ou
égal à p, donc supérieur à n. On a donc démontré:
si P admet plus de n racines, son degré est supérieur à
n. La contraposée de cette proposition donne la conclusion.
2°) Ordre de multiplicité d'une racine : on dit que a
est une racine de P d'ordre de multiplicité k ssi : P(x) = (x -
a
)kQ(x), avec Q(a ) non nul.
Si a est d'ordre 1, on dit que a
est une racine simple. Si a est d'ordre 2, on
dit que a est une racine double.
Exemple : Soit P(x) = ax2 + bx + c avec a non nul, et soit
D
= b2 - 4ac.
Si D > 0 , P admet deux racines simples
x1 et x2, et P(x) = a(x - x1)(x -x2).
Si D = 0, P admet une racine double x1
, et
P(x) = a(x -x1)2.
En reprenant la démonstration du 1°), et sans plus supposer
que les racines sont distinctes, on obtient :
Un polynôme de degré n ³ 1
admet au plus n racines, chaque racine étant comptée avec
son ordre de multiplicité
3°) algorithme
de Horner
a) Calcul de P(a ).
· Dans un premier temps, considérons
P polynôme de degré 3 :
P(x) = a3x3
+ a2x2 + a1x + a0
Soit Q(x) = P(x) - P(a ). Q est un polynôme
et Q(a ) = 0. Donc, d'après le théorème
fondamental (voir plus haut) :
Q(x) = (x - a
) R(x)
R(x) est de degré 2 : R(x) = b2x2 + b1x
+ b0. On a donc :
P(x) - P(a
) = (x - a ) (b2x2
+ b1x
+ b0)
a3x3
+ a2x2 + a1x + a0
- P(a ) = (x - a
) (b2x2 + b1x + b0)
a3x3
+ a2x2 + a1x + a0
- P(a ) = b2x3
+ (b1 -a b2)x2
+ (b0 - a b1)x -
a
b0
Par identification, on obtient le système (d'inconnues b0,
b1, b2, P(a ) ) :

qui se résout en cascade pour donner :

Disposition pratique :

(Les flèches indiquent une multiplication par a
.)
· Dans un deuxième temps, étudions
la généralisation à P polynôme de degré
n :
P(x) = anxn
+ ... + a1x + a0
Soit Q(x) = P(x) - P(a ). Q est un polynôme
et Q(a ) = 0. Donc, d'après le théorème
fondamental :
Q(x) = (x - a
) R(x)
R(x) est de degré n - 1 : R(x) = bn-1xn-1 +
... + b1x + b0. On a donc :
P(x) - P(a
) = (x - a ) (bn-1xn-1
+
... + b1x + b0)
anxn
+ ... + a1x + a0 - P(a
) = (x - a ) (bn-1xn-1
+
... + b1x + b0)
anxn
+ ... + a1x + a0 - P(a
) = bn-1 xn + (bn-2 -a
bn-1)xn-1 + ... + (b0 - a
b1)x - a b0
Par identification, on obtient le système ( d'inconnues b0,
b1, ... , bn-1, P(a )
) :
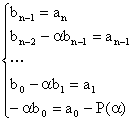
qui se résout en cascade pour donner :

Ceci aboutit à l'algorithme de Horner proprement dit pour le
calcul de P(a ) :
| variables d'entrée : |
n, degré du polynôme P
a[0], a[1], ... , a[n], les coefficients de P
alpha |
| variables de sortie : |
x ( = P(alpha) ) |
| traitement : |
lire n , a[0],
a[1], ... , a[n] , alpha ;
x ¬ a[n] ;
Pour i variant de n -1 à 0 faire x ¬
a[i] + alpha * x ;
écrire x ; |
Cela donnera en turbo-pascal :
program horner ;
var n,i:integer;alpha,x:real;a:array[0..100]of real;
BEGIN
writeln('degré du polynôme P ?);readln(n);
writeln('écrire les coeff du polynôme suivant les puissances
croissantes');
for i:= 0 to n do read(a[i]);
write('alpha=');readln(alpha);
x:=a[n];
for i:= n-1 downto 0 do x:=a[i]+alpha*x;
write('P(alpha)=',x);
END.
Remarque : le sens de : "for
i:= n-1 downto 0 do"
est assez évident : pour i variant
en
descendant de n- 1 à 0, faire". Mais le "downto" est indispensable
: "for i:= n-1 to 0 do" donnerait
une boucle vide.
b) Factorisation de P
Reprenons l'exemple d'un polynôme de degré 3 :
P(x) = a3x3
+ a2x2 + a1x + a0
Gardons les mêmes notations, et supposons que a
soit racine de P. On observe alors que l'on a obtenu une factorisation
de P :
P(x) = (x - a
) (b2x2 + b1x + b0),
car b0, b1, b2 sont fournis par l'algorithme.
Voyons sur un exemple :
P(x) = 2x3 -5x
-3
-1 est racine de P, l'algorithme (ou schéma...) fournit :
| 2 |
0 |
-5 |
-3 |
| |
-2 |
2 |
3 |
| 2 |
-2 |
-3 |
0 |
P(-1) est bien égal à 0, et on a obtenu :
P(x) = (x + 1) (2x2
- 2x - 3)
2x2 - 2x - 3 admet deux racines simples : a1
= (1 -Ö 7)/2 et a2
= (1 + Ö 7)/2, la factorisation complète
de P est donc :
P(x) = 2(x + 1)(x-a1)(x
- a2)
IV. espace vectoriel R[x]
Proposition 1 : a) L'ensemble R[x] des polynômes
à coefficients réels est une espace vectoriel pour les opérations
usuelles :
(P + Q)(x) = P(x) + Q(x), (l P)(x) = l
P(x).
b) R[x] est de dimension infinie, sa base canonique est : (1,
x, x2, ..., xn, ...).
Dem :
a) R[x] est en effet un sous-espace vectoriel de l'espace vectoriel
des fonctions de R dans R : R[x] est non vide (il
contient le polynôme nul), la somme de deux polynômes est un
polynôme, le produit d'un polynôme par un réel est un
polynôme.
b) Tout polynôme P est combinaison linéaire (finie) de
1, x, x2, ..., et ceci de façon unique : c'est pratiquement
la définition d'un polynôme...
Remarquons que de plus le produit et la composée de deux éléments
de R[x] est un élément de R[x].
Proposition 2 Pour n dans N, l'ensemble Rn[x]
des
polynômes de degré £ n est
un espace vectoriel pour les opérations usuelles. Rn[x]
est
de dimension n + 1, de base canonique (1, x, x2, ..., xn).
Dem :
Il suffit de démontrer que Rn[x] est un sev
de R[x] : Rn[x] est non vide (il contient le polynôme
nul), et si d°(P) £ n, d°(Q) £
n, alors d°(P + Q) £ n, et d°(l
P) £ n, avec l
réel.
On peut bien sûr considérer des applications linéaires
sur ces espaces vectoriels. A titre d'illustration, considérons
l'exercice suivant :
Soit j l'application de Rn[x]
dans R[x] définie par :
j
(P)(x) = P(x + 1)
a) Déterminer j (P) avec : P(x) =
1, P(x) = x, P(x) = xn, P(x) = x - 1.
b) Montrer que j est un automorphisme de
Rn[x].
c) Déterminer la matrice de j dans
la base canonique de Rn[x], déterminer j-1,
puis sa matrice. En déduire que le tableau de Pascal à l'ordre
n définit une matrice inversible, et donner son inverse !
Solution :
a) Si P(x) = 1 pour tout x, alors P(x + 1) = 1, donc j
(P)(x) = 1 pour tout x.
Si P(x) = x pour tout x, alors P(x + 1) = x + 1, donc j
(P)(x) = x + 1.
Si P(x) = xn pour tout x, alors P(x + 1) = (x + 1)n,
donc j (P)(x) = (x + 1)n.
Si P(x) = x - 1 pour tout x, alors P(x + 1) = x - 1 + 1 = x.
b) Il y a en fait trois choses à démontrer :
(i) j est une application
de Rn[x] dans Rn[x]
(ii) j est linéaire
(iii) j est bijective
(i) j est une application de Rn[x]
dans
Rn[x].
Soit P un polynôme de degré £
n :
P(x) = a0 + a1x
+ a2x2 + ... + anxn
Alors j (P)(x) = P(x + 1) = a0
+ a1(x + 1) + a2 (x + 2)2 + ... + an(x
+ 1)n
Donc j (P) est un polynôme de degré
£
n.
(ii) j est linéaire. Soit P et Q deux
polynômes de degré £ n.
| j (P + Q)(x) |
= (P + Q)(x + 1) |
par définition de j |
| |
= P(x + 1) + Q(x + 1) |
par définition de P + Q |
| |
= j (P)(x) + j
(Q)(x) |
par définition de j |
Donc j (P + Q) = j
(P) + j (Q). De même j
(l P) = lj (P), et
j
est linéaire.
(iii) j est bijective. En effet, pour Q quelconque
dans Rn[x] :
j
(P)(x) = Q(x) Û P(x + 1) = Q(x) Û
P(x) = Q(x - 1)
Q admet donc un antécédent unique P, appartenant à
Rn[x],
défini par P(x) = Q(x - 1).
c) On obtient la matrice de j dans la base
canonique de Rn[x] en écrivant en colonne les
coordonnées de j (1), j
(x), ... ,
j (xn) dans la base 1, x, ...
, xn. (Attention, il s'agit des polynômes
1, x, ... , xn, et non des nombres réels 1, x, ... ,
xn.) Comme
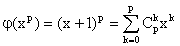
pour tout p appartenant à {0, 1, ... , n}, (formule du binôme),
on obtient, en notant A la matrice recherchée :
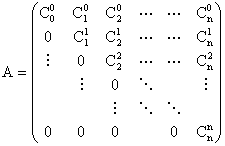
On a déterminé dans le b) la bijection réciproque
de j : j-1(P)
(x) = P(x - 1). On obtient A-1 en écrivant en colonne
les coordonnées de j-1(1),
j-1(x),
... , j-1(xn) dans la
base 1, x, ... , xn. Comme

On obtient :

A est le tableau de Pascal (après transposition dans sa présentation
traditionnelle), et A-1 est l'inverse du tableau de Pascal...
Exemple avec n = 4 :

Et on vérifie que ça marche !
Remarque : On peut dire directement que le tableau de Pascal à
l'ordre n constitue une matrice inversible, et plus précisément
que sa seule valeur propre est 1, pourquoi ? Cette matrice est-elle diagonalisable
?