I. fonctions sinus et cosinus
II. fonctions tangente
Définition
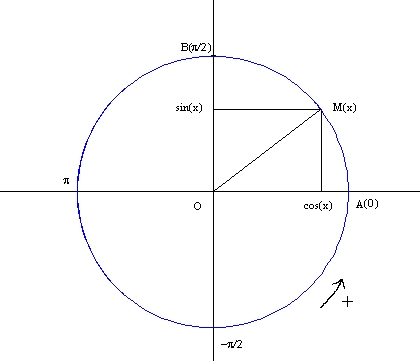
Le cercle trigonométrique est un cercle de centre O,
de rayon 1, muni d'un sens de parcours (le fameux "sens contraire des aiguille
d'une montre"), et d'un repère orthonormé direct R
= ![]() (on
passe de OA à OB en faisant un "quart de tour à droite").
(on
passe de OA à OB en faisant un "quart de tour à droite").
Un point M du cercle est repéré par x, une des
distances parcourues sur le cercle pour aller de A à M, affectée
du signe "+" si on parcourt le cercle dans le sens direct, et du signe
"-" si on le parcourt dans le sens rétrograde. On note M(x).
Par définition, si M(x), alors les coordonnées
de M dans le repère R sont (cos(x), sin(x)).
Etude
· Propriétés visibles
sur le cercle trigonométrique :
* Ensemble de définition. On peut parcourir indéfiniment
le cercle dans un sens ou dans l'autre, par conséquent :
cos(x) et sin(x) sont définis pour tout x dans R
* Valeurs prises par cos(x) et sin(x). Le cercle est
de rayon 1, donc :
pour tout x dans R : -1 £ cos(x) £
1 ; -1 £ sin(x) £
1
* Périodicité. Si M(x), comme la longueur du cercle
est 2p .1 = 2p ,
alors aussi M(x + 2p ), M(x-2p
), et plus généralement M(x + 2kp
), k entier relatif. Par conséquent :
Les fonctions cosinus et sinus sont périodiques de période
2p :
Pour tout x dans R : cos(x + 2p ) = cos(x -2p
) = cos(x)
sin(x + 2p ) = sin(x - 2p
) = sin(x)
* Parité. Les points M(x) et M '(-x) sont symétrique
par rapport à l'axe des abscisses, donc :
cos est une fonction paire, sin est une fonction paire :
pour tout x dans R : cos(-x) = cos(x) ; sin(-x) = -sin(x)
* Valeurs remarquables. On a : A(0), B(p
/2), etc : il est facile de trouver les valeurs des cosinus et sinus des
multiples de
p /2 :
cos(0) = 1 sin(0) = 0
cos(p /2) = 0 sin(p
/2) = 1
cos(p ) = -1 sin(p
) = 0
cos(3p /2) = 0 sin(3p
/2) = -1
e.t.c
* Relation fondamentale de la trigonométrie. Le théorème
de Pythagore appliqué au triangle rectangle OHM, ave H le point
de coordonnées (cos(x), 0) conduit à :
pour tout x dans R : (cos(x))2 + (sin(x))2 = 1
Soit, en notant cos2x = (cos(x))2 :
pour tout x dans R : cos2x + sin2x = 1
* Signe de cos(x), sin(x).
pour 0 £ x £p
/2 : cos(x) ³ 0 sin(x) ³
0
pour p /2 £
x £ p : cos(x)
£
0 sin(x) ³ 0
pour p £ x
£
3p /2 : cos(x)
£
0 sin(x) £ 0
pour 3p /2 £
x £ 2p : cos(x)
³
0 sin(x) £ 0
e.t.c
* On peut encore "voir" d'autres propriétés, comme par
exemple :
pour tout x dans R : cos(x + p ) = -cos(x),
sin(x +p ) = -sin(x)
Retenons celle-ci, utile pour l'étude de la fonction tangente.
· Autres propriétés
analytiques :
* Continuité, dérivabilité : On admet :
Les fonctions cos et sin sont dérivables sur R
Pour tout x réel : cos'(x) = -sin(x) ; sin'(x) = cos(x)
Il en résulte que les fonctions cos et sin sont continues
sur R, d'une part, de classe C¥sur
R,
d'autre part.
* Sens de variation. A cause de la périodicité,
l'étude sur l'intervalle (de longueur 2p
) [-p , p ] suffit.
A cause des propriétés de parité, on peut réduire
l'intervalle d'étude à [0, p ].
On obtient alors :

* Représentation graphique :

* Etude en 0
La fonction sin est dérivable 0, de dérivée cos
0 = 1, donc :
![]()
· Propriétés avancées
:
* DL de sin(x) en 0 : (n appartient à N)
![]()
On retrouve avec n = 0, au voisinage de 0 : sin(x) ~ x
* DL de cos(x) en 0 :
![]()
On en déduit, avec n = 2, au voisinage de 0 : 1 - cos(x) ~ x2/2
I. fonctions sinus et cosinus
II. Fonction tangente
Définition
![]()
Etude
* cos(x) = 0 ssi x = p /2 + kp
, k appartenant à Z. Par conséquent :
La fonction tan est définie sur D = R \ {p
/2 + kp ; k dans Z}
* Pour tout x dans D, x + p et x - p
appartiennent à D, et
![]()
La fonction tan est périodique de période p
* Pour tout x dans D, -x appartient à D, et tan(-x)= sin(-x)/cos(-x)
= -sin(x)/cos(x) = -tan(x)
La
fonction tan est impaire
* Sur D, tan est le quotient de deux fonctions dérivables avec
le dénominateur qui ne s'annule pas, et :
![]()
Comme d'autre part, cos2x + sin2x = 1, on a aussi : tan'x = 1/cos2x.
![]()
* Il suffit d'étudier tan sur [0, p
/2[ :
tan(0) = 0
tan' > 0 sur D, donc tan est strictement croissante sur [0, p
/2[
sin(x) tend vers 1 quand x tend vers p /2,
cos(x) tend vers 0+ quand x tend vers (p
/2)-, donc tan(x) tend vers +¥
quand x tend vers (p /2)-
* Représentation graphique :
