retour à l'index cours
retour à l'accueil
 

I. Espaces vectoriels, sous-espaces vectoriels

Rappel : on sait additionner deux vecteurs du plan, multiplier un vecteur du plan par un nombre réel.

1°) Espaces vectoriels

Définition Un espace vectoriel E sur R est un ensemble contenant au moins un élément, noté 0, et muni de deux opérations : une addition (interne) : u Î E, v Î E, u + v Î E, une multiplication (externe) par les scalaires lÎR : u Î E, l Î R, l .u Î E, avec les propriétés suivantes :
Pour u,v Î E, a , b Î R :
    u + (v + w) = (u + v) + w = u + v + w
    u + v = v + u
    u + 0 = 0 + u = u
    u + (-u) = (-u) + u =0
    (a + b ).u = a .u + b .u
    a .(u + v) = a .u + a .v
    a .(b .u) = (ab ).u
    1.u = u

Les quatre premières propriétés définissent la structure de groupe commutatif.

Propriétés On a 0.u = 0, a .0 = 0 et a.u = 0 Þ a = 0 ou u = 0. Attention, pour A, B matrices, AB = 0 n'implique pas A = 0 ou B = 0. D'autre part, le même signe, '0', désigne à la fois le nombre réel 0 et l'élément neutre de l'espace vectoriel E. Dans la pratique, cela ne prête pas à confusion.

Exemples d'espaces vectoriels
· R² = {(x,y) ; x Î R, y ÎR} est un e.v pour les opérations :
    (x,y) + (x',y') = (x+x',y+y')
       a .(x,y) = (a x,a y)
x et y sont les composantes de (x,y).
Idem pour R³, R⁴, et plus généralement pour Rⁿ, n Î N, avec R¹ = R, R⁰ = {0}.

· L'ensemble S des suites réelles est un e.v pour les opérations :
    (u_n) + (v_n) = (u_n +v_n)
       a .(u_n) = (a u_n)

· L'ensemble F(I, R) des applications de l'intervalle I dans R est un e.v pour les lois :
    (f + g) (x) = f(x) + g(x)
    (a .f)(x) = a f(x)
F(I, R) est noté aussi R^I.

· L'ensemble P des polynômes réels (noté aussi R[X]) est un e.v pour les mêmes lois que ci-dessus. (C'est d'ailleurs un sous-espace vectoriel de F(R,R), voir plus loin.)

· L'ensemble M_n,p(R) des matrices à n lignes et p colonnes est un e.v pour l'addition des matrices et la multiplication des matrices par un réel.

· L'ensemble des variables aléatoires sur un espace probabilisé (W , T, P) est un e.v pour les opérations X + Y, a .X.

2°) Sous-espaces vectoriels
Définition Soit E un e.v, et F Ì E. On dit que F est un sev de E ssi F est lui-même un e.v

Théorème Soit E un e.v, et F Ì E. F est un sev de E ssi :
    F est non vide
    u, v Î F Þ u +v Î F
    u Î F, aÎR Þ a .u Î F

Exercice On montrera que les ensembles suivants sont des sev d'un certain e.v, donc des e.v ...
E₁ = {(u_n) ; " n ÎN u_n+2 = -2u_n+1 + 3u_n} ; E₂ = { ; a,b,c,d ÎR, a+d = 0} ;
P l'ensemble des polynômes réels ;
P₂ l'ensemble des polynômes réels de degré £ 2 ;
Cⁿ( I ) l'ensemble des fonctions de classe Cⁿ sur l'intervalle I, n Î N È {¥ }. On précisera l'inclusion l'un dans l'autre de ces divers espaces.

3°) Notion de combinaison linéaire

Soit u₁, u₂, ... ,u_n des vecteurs de E. Tout vecteur de la forme x₁.u₁ + x₂.u₂ + ... +x_n.u_n est une combinaison linéaire de u₁, u₂, ... ,u_n. Les réels x₁, x₂, ... , x_n sont les coefficients de la combinaison linéaire.

Exercice 1°)Soit u₁ = (1, -2), u₂ = (3, -4) , v = (5, 6). Montrer que v est c.l de u₁ et u₂, et ceci de façon unique. Plus généralement, montrer que tout vecteur w = (a , b ) est c.l de u₁ et u₂, de façon unique.
2°) Soit u₁ = (2, -1) , u₂ = (-4, 2). Montrer que 0 est c.l de u₁ et u₂, mais pas de façon unique. Montrer qu'il y a dans R² deux sortes de vecteurs : ceux qui sont c.l de u₁ et u₂, mais pas de façon unique, et ceux qui ne le sont pas du tout...
3°) Soit u₁ = (2, 1,-3), u₂ = (3, 5, -2). Montrer que 0 est c.l de u₁ et u₂, et ceci de façon unique. Montrer qu'il y a dans R³ deux sortes de vecteurs : ceux qui sont c.l de u₁ et u₂, et ceci de façon unique, et ceux qui ne le sont pas du tout...

II. Familles libres, génératrices, bases

La situation mise en évidence dans l'exercice précédent semble inextricable. D'autre part, il est important pour les applications de trouver des familles de vecteurs ayant la propriété suivante : tout vecteur de E est c.l des éléments de la famille, de façon unique. Tout ceci conduit aux ...

Définitions Soit F = {u₁, u₂, ... ,u_n}une famille de vecteurs de E. La famille F est dite :
* libre ssi 0 est c.l de u₁, u₂, ... ,u_n de façon unique :
    x₁.u₁ + x₂.u₂ + ... +x_n.u_n = 0 Þ x₁ = x₂ =... = x_n = 0.
On dit aussi que u₁, u₂, ... ,u_n sont linéairement indépendants.
* liée ssi F n'est pas libre.
* génératrice de E ssi tout vecteur de E est c.l de u₁, u₂, ... ,u_n.
* une base de E ssi tout vecteur v de E est c.l de u₁, u₂, ... ,u_n, et ceci de façon unique :
    " v Î E  $ ! (x₁, x₂, ... ,x_n) ÎRⁿ   v = x₁.u₁ + x₂.u₂ + ... +x_n.u_n .
Les réels x₁, x₂, ... , x_n sont appelés les coordonnées de v dans la base F. On note
    v_F(x₁, x₂, ... , x_n) .

... Et au ...
Théorème Dans un espace vectoriel E, toutes les bases ont le même nombre d'éléments. Ce nombre est appelé la dimension de E. Soit n la dimension de E et soit F une famille d'éléments de E. Chacune des propriétés de F ci-dessous implique toutes les autres :
    libre et à n éléments
    génératrice de E et à n éléments
    libre et génératrice de E
    base de E

Exemples
* La famille (u) est libre ssi u ¹0.
* La famille (u, v) est libre ssi u et v ne sont pas colinéaires. Dans E = Rⁿ, cela signifie que les composantes de u et v ne sont pas proportionnelles :
    ( (2, 1, -3) , (-4, -2, 6) ) est une famille liée,
    ( (2, 1, -3) , (-4, -2, 5) ) est une famille libre.
Attention, ceci ne se généralise pas à trois vecteurs : on peut avoir u, v, w non colinéaires deux à deux, et (u, v, w) liée.

* Rⁿ est un e.v de dimension n, {0} est un e.v de dimension 0.

* Dans R³, B = (e₁, e₂, e₃), avec e₁ = (1, 0, 0), e₂ = (0, 1, 0), e₃ = (0, 0, 1), est la base canonique de R³, ainsi appelée car les composantes de v coïncident avec les coordonnées de v dans la base B :
    (2, 1, -3) = 2. (1, 0, 0) +1.(0, 1, 0) - 3.(0, 0, 1)

* R_n[x], ensemble des polynômes de degré inférieur ou égal à n, est un espace vectoriel de dimension n + 1. Sa base canonique est :
    B = (1, x, x², ... , xⁿ).
En effet, tout polynôme de degré inférieur ou égal à n est combinaison linéaire de 1, x, x², ... , xⁿ, et ceci de façon unique...

* M_n,p(R), ensemble des matrices réelles à n lignes et p colonnes, est un espace vectoriel de dimension np. Par exemple,  M_2,2(R) ( noté aussi M₂(R) ) est un espace vectoriel de dimension 4, dont la base canonique est formée des matrices :

Orientation
Dans un ev E de dimension n, une famille libre a au plus n vecteurs ; elle peut être complétée en une base de E (théorème de la base incomplète). Une famille génératrice a au moins n vecteurs ; on peut en extraire une base de E.

Sous-espace vectoriel engendré par une famille de vecteurs
Soit F une famille de vecteurs de E. L'ensemble de c.l des vecteurs de F est un sev de E, appelé sev engendré par F.

Exercice : Soit F = { (x, y,z) Î R³ ; 2x +y +z = 0 } ; Montrer que F est un sev de R³, déterminer une base et la dimension de F.

III. Applications linéaires

Définition Soit E et F deux e.v. Une application f : E ® F est dite linéaire ssi :
u,v Î E f(u + v) = f(u) + f(v)
u Î E " x Î R f(x.u) = x.f(u)

Propriétés
* f(0_E) = 0_F
* f(-u) = -f(u)
* f linéaire ssi, pout tout x_i dans R pour tout u_i dans E :

(l'image d'une combinaison linéaire est la combinaison linéaire des images)

Exemples

* 0 :		Id :		sont des applications linéaires

* (important) Une application linéaire est entièrement déterminée par la connaissance des images des vecteurs d'une base. Par exemple, soit B = (e₁, e₂) la base canonique de R², f : R² ® R² linéaire telle que f(e₁) = (2,3), f(e₂) = (4,-5). Alors pour tout u = (x,y) Î R² :
    f(u) = f( (x,y) ) = f( x.e₁ + y.e₂) = x.f(e₁) + y.f(e₂) = x.(2,3) + y(4,-5) = (2x+4y,3x-5y)
Disposition pratique : Soit
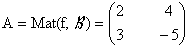(matrice de f dans la base B)
(matrice-colonne de u dans la base B)
(matrice-colonne de f(u) dans la base B)

Alors AX = Y :

Remarque : la matrice unité I est la matrice de l'application linéaire Id_E dans toute base de l'espace vectoriel E, la matrice nulle est la matrice de l'application linéaire nulle dans toute base de E.

IV. Espace vectoriel L(E,F), algèbre L(E)

Théorème 1 Soit E et F deux espaces vectoriels, B une base de E, C une base de F. L'ensemble L(E,F) est une espace vectoriel.
De plus, avec f, g Î L(E,F), aÎR, si A = Mat(f, B, C), B = Mat(g, B, C), alors :
A + B = Mat(f + g, B, C),
a .A = Mat(a .f, B, C)

Théorème 2 Soit L(E) l'espace vectoriel des applications linéaires de E dans E.Soit f, gÎL(E). Alors fog Î L(E). De plus :
Si A = Mat(f, B), B = Mat(g, B), alors AB = Mat(fog, B) ;
f bijective Û A inversible, et on a alors A^-1 = Mat(f ^-1, B).

Vocabulaire Soit f : E ® F linéaire

	cas général	f bijective
cas général	homomorphisme	isomorphisme
E = F	endomorphisme	automorphisme

Une application linéaire de E dans R est une forme linéaire. Exemples :
* Les formes linéaires de R³ dans R sont les applications (x, y, z) ® ax + by + cz . Elles sont représentées par les matrices lignes 
* (fondamental) Soit E l'espace vectoriel des v.a discrètes définies sur un espace probabilisé (W , P(W ), P), W fini. Alors l'espérance E : E ®R est une forme linéaire :
    E(X + Y) = E(X) + E(Y), E(a X) = a E(X).
* (fondamental) Soit E l'espace vectoriel des fonctions continues sur l'intervalle fermé borné[a, b]. Alors l'intégrale :

    E ®R

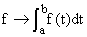
définit une forme linéaire sur E :

V. Noyau et image d'une application linéaire

Soit f : E ® F linéaire
Définitions Im(f) = {v Î F ; $ u Î E, f(u) = v } (image de f)
Ker(f) = {u Î E ; f(u) = 0_F} (noyau de f)

Théorème a) Ker(f) est un sev de E. Im(f) est un sev de F ; si (u₁, u₂, ... , u_n) est une base de E, Im(f) est engendré par f(u₁), f(u₂), ... , f(u_n).
b) (formule du rang) dim( Im(f) ) + dim( Ker(f) ) = dim(E)

Dem a) Ker(f) est non vide car f(0_E) = 0_F donc 0_E Î Ker(f) ; si u,v Î Ker(f) et a ÎR, alors :
f(u + v) = f(u) + f(v) = 0_F + 0_F = 0_F donc u + v Î Ker(f) ;
f(a .u) = a .f(u) = a .0_F = 0_F donc a .u Î Ker(f).
Im(f) est non vide car f(0_E) = 0_F donc 0_FÎ Im(f) ; si u',v' Î Im(f) et aÎR, alors :
u' + v' = f(u) + f(v) = f(u + v) donc u' + v' Î Im(f) ;
a .u' = a .f(u) = f(a .u) donc a .u' Î Im(f).
b) Soit n la dimension de E, et soit (u₁, u₂, ... , u_p) une base de Ker(f) ; (u₁, u₂, ... , u_p) est une famille libre, d'après le théorème de la base incomplète, il existe des vecteurs u_p+1, u_p+2, ... ... ,u_n tels que (u₁, u₂, ... , u_p, u_p+1, u_p+2, ... ... ,u_n) soit une base de E.

( f(u_p+1), f(u_p+2), ... ,f(u_n) ) est une famille génératrice de Im(f), or cette famille est libre :
C'est donc une base de Im(f), qui est donc de dimension n - p. Comme Ker(f) est de dimension p et E de dimension n, on a bien dim( Im(f) ) + dim( Ker(f) ) = dim(E).

Rappel Soit f : E ® F une application. f est dite :
injective ssi f(x) = f(x') Þ x = x' ;
surjective ssi " y Î F $ x Î E, f(x) = y ;
bijective ssi " y Î F $ x Î E, x unique, f(x) = y.

Propriété : f bijective Û f injective et surjective.

Théorème Soit f : E ® F linéaire.
a) f injective Û Ker(f) = {0_E};
b) f surjective Û Im(f) = F.

Dem a) Supposons f injective ; soit x Î Ker(f) ; alors :
f(x) =0_F, f(0_E) = 0_F et f injective, donc x = 0_E,et Ker(f) = {0_E}.
Réciproquement, supposons Ker(f) = {0_E}. Soit x, x' tel que f(x) = f(x') ; alors :
f(x) - f(x') = 0_F, f(x -x') = 0_F, x -x' Î Ker(f), x - x' = 0_E car Ker(f) = {0_E}, x = x', donc f est injective.
b) f surjective Û Im(f) = F par définition de "f est surjective".

Corollaire a) Soit f un ENDOMORPHISME de E ; alors :
f bijective Û f surjective Û f injective Û Ker(f) = {0}.
b) Soit f : E ® F linéaire ; alors :
f bijective Û f injective ( Û Ker(f) = {0}) et dim(F) = dim(E).

Dem appliquer la formule du rang.

Savoir-faire Montrer qu'un ENDOMORPHISME f : R³®R³ est bijectif :

· A = Mat(f, B) est inversible :	* méthode du pivot
	* $ A'     A.A' = I (et alors A' = A-1)
	* $ A'     A'.A = I (et alors A' = A-1)

· f est injective ( Û Ker(f) = {0}) Û L'équation AX = 0 admet 0 pour unique solution
· f est surjective ( Û Im(f) = R³)
· l'image par f d'une base de R³ est une base de R³

VI. Calcul matriciel

Règles de calcul
M_n(R), ensemble des matrices carrées d'ordre n a coefficients dans R, est un espace vectoriel de dimension n². De plus :
A(B + C) = AB + AC
(A + B)C = AC + BC
(AB)C = A(BC) = ABC
l .(AB) = (l .A)B = A(l .B)
AI = IA = A (I matrice unité)

Attention ! AB ¹ BA en général ; si AB = BA, on dit que les matrices A et B commutent.
AB = 0 n'implique pas A = 0 ou B = 0.
AB = AC n'implique pas B = C, même si A ¹ 0.

Matrices inversibles, inverse d'une matrice
* A Î M₃(R) est inversible
Û $ A^-1Î M₃(R), A.A^-1 = A^-1.A = I (définition)
Û $ A' Î M₃(R), A.A' = I, et alors A' = A^-1 (La recherche effective de A' se fait en utilisant la méthode du pivot)

Û Avec A = Mat(f, B), f est bijective

* Si A.B = I, alors A est inversible et A^-1 = B
* Si A.B = 0 avec B ¹0, alors A n'est pas inversible (raisonner par l'absurde).
* (très important) Une matrice TRIANGULAIRE est inversible ssi il n'y a pas de zéros sur la diagonale ; une matrice avec une ligne ou une colonne de zéros n'est pas inversible. Ces deux propriétés sont utilisées dans la recherche des valeurs propres d'une matrice.
* Si A et B sont inversibles, alors AB est inversible, et (AB)^-1 = B^-1A^-1 (vérifier !)

Puissance n-ième d'une matrice
A⁰ = I et Aⁿ = AA ... A (n facteurs) pour n ³ 1.
(A^-1)ⁿ = (Aⁿ)^-1 = A^-n pour A inversible et n Î N.
(Aⁿ)^p = A^np pour n, p ÎN ( ÎZ si A inversible)
formule du binôme : Avec A, B qui commutent et n ÎN:

retour début